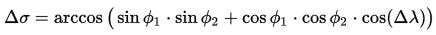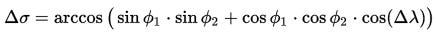Calculating Great Circle Distances in Python
The shortest distance between two locations on the surface of Earth (or any planet) is known as the Great Circle Distance. Except for relatively short distances these cannot be measured on a map due to the distortion and flattening necessary to represent a sphere on a flat plane. However, the calculation of the Great Circle Distance from two coordinates is simple, although I suspect generations of midshipmen might not have agreed. In this post I will write a short program in Python to calculate the distance from London to various other cities round the world.
As always, Wikipedia provides a comprehensive reference on the subject of calculating Great Circle distances. The principle is very simple, if you understand radians.
Everyone is familiar with using degrees to measure angles - we all gain an understanding of them when we are given our first school protractor. Slightly less well understood is the radian. (If you already know all about radians skip to the next paragraph!) Imagine a circle (for the purposes of this project, imagine the circle is the flat part of a hemisphere, a sphere cut in half) and now imagine drawing a line from the centre to the edge. The length of that line is of course the radius. Now draw round the circumference of the circle by the same distance as the radius, finally drawing another line back to the centre of the circle. The angle between the two lines meeting at the centre is 1 radian. The size of 1 radian in degrees is 180/π which is an irrational number but 57.29577951° to 8dp.
If you skipped my scholarly discourse on radians, welcome back. If you think about it for a moment, it should become clear that if the angle between two points on the surface of our little blue planet is 1 radian, then the great circle distance between them is the same as the radius of the planet. If the angle is 2 radians, the distance is twice the radius; if the angle is 0.5 radians the distance is half the radius and so in. In short, the Great Circle Distance between two points in the angle between them multiplied by the radius. The units of distance are irrelevant as long as they are the same (don't mix miles and kilometres for example) but we must use radians rather than degrees. This is the reason we are using radians - they reduce the problem to one simple multiplication.
We're getting ahead of ourselves a bit here, as we first need to calculate the angle between two points from their latitudes and longitudes. I'll "borrow" the formula for this from Wikipedia, but first let's define some terms.
Φ1 and λ1 - latitude and longitude in radians of first location
Φ2 and λ2 - latitude and longitude in radians of second location
ΔΦ and Δλ - absolute differences between latitudes and longitudes
Δσ - angle between locations
Don't worry, I won't be using Greek in the code. Now for the formula - note use of dot notation for multiplication.
So basically we need to apply this formula to a pair of coordinates, then multiply the result by the radius of the Earth.
The Code
The code consists of the following two files which you can grab from the Github repository.
greatcircle.py
greatcircledemo.py
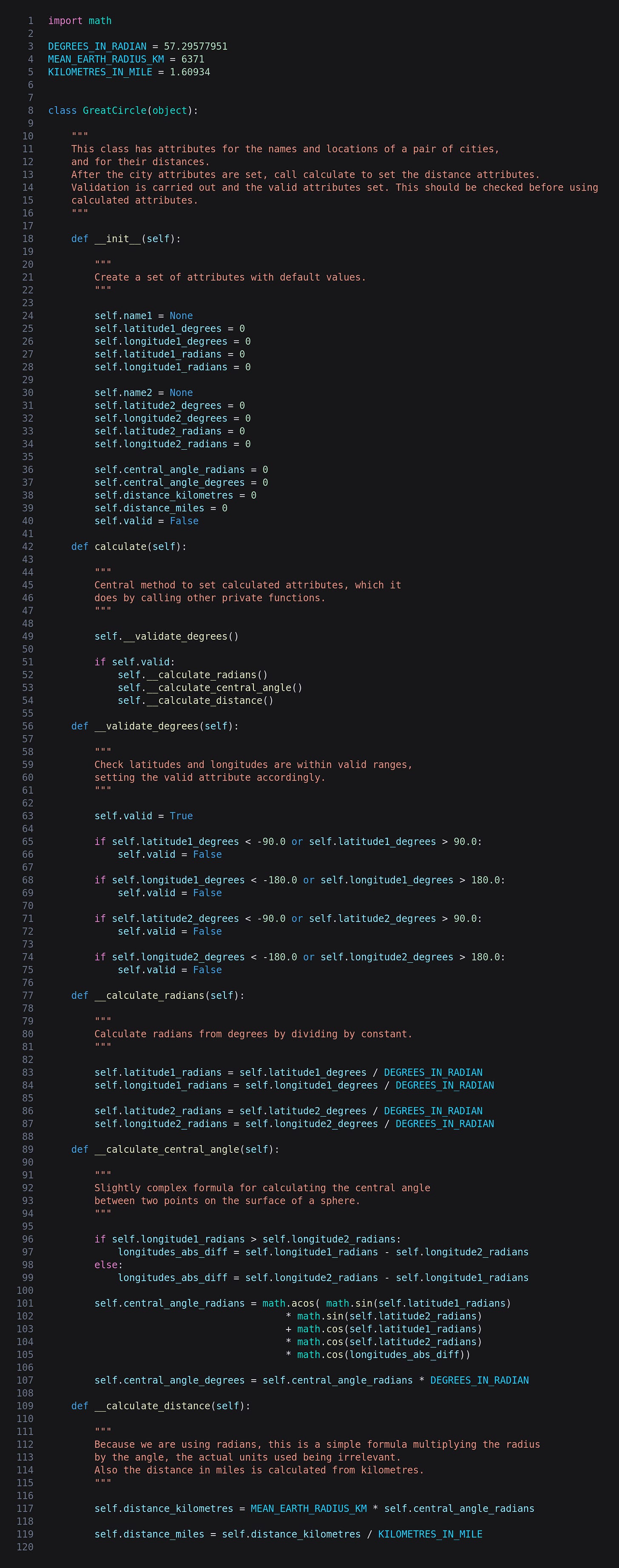
This is greatcircle.py.
The first thing to note is that we create and initialize a few variables (or "pseudo-constants" denoted by upper case names) for later use: DEGREES_IN_RADIAN, MEAN_EARTH_RADIUS_KM and KILOMETRES_IN_MILE.
The main functionality is contained in a class called GreatCircle, and in __init__ we create a number of properties with default values. Most pieces of information exist twice: the latitudes, longitudes and angle in both radians and degrees, and the distance in miles and kilometres. There is also a boolean valid flag, a single method called calculate, and a few private functions (denoted with the double underscore or "dunder" prefix).
The greatcircle_calculate function is central to the whole project as it calculates the missing values from the latitudes and longitudes in degrees. Before it does this it checks the degrees are valid with the validate_degrees function, and if so calls calculate_radians, calculate_central_angle and calculate_distance.
Now let's move on to the four private functions called by greatcircle_calculate. The first is validate_degrees which simply checks the latitudes are between -90° and +90°, and that the longitudes are between -180° and +180°.
The calculate_radians function does its stuff by dividing the degrees by DEGREES_IN_RADIAN which was initialised at the top of the file.
The calculate_central_angle function calculates the absolute difference between the longitudes, and then implements this formula:
which we saw above to actually calculate the angle in radians. Finally it calculates the degree equivalent.
The last function in this file is calculate_distance, which as I have mentioned is simply a matter of multiplying the angle in radians by the radius of the earth. We also do the kilometres to miles conversion here.
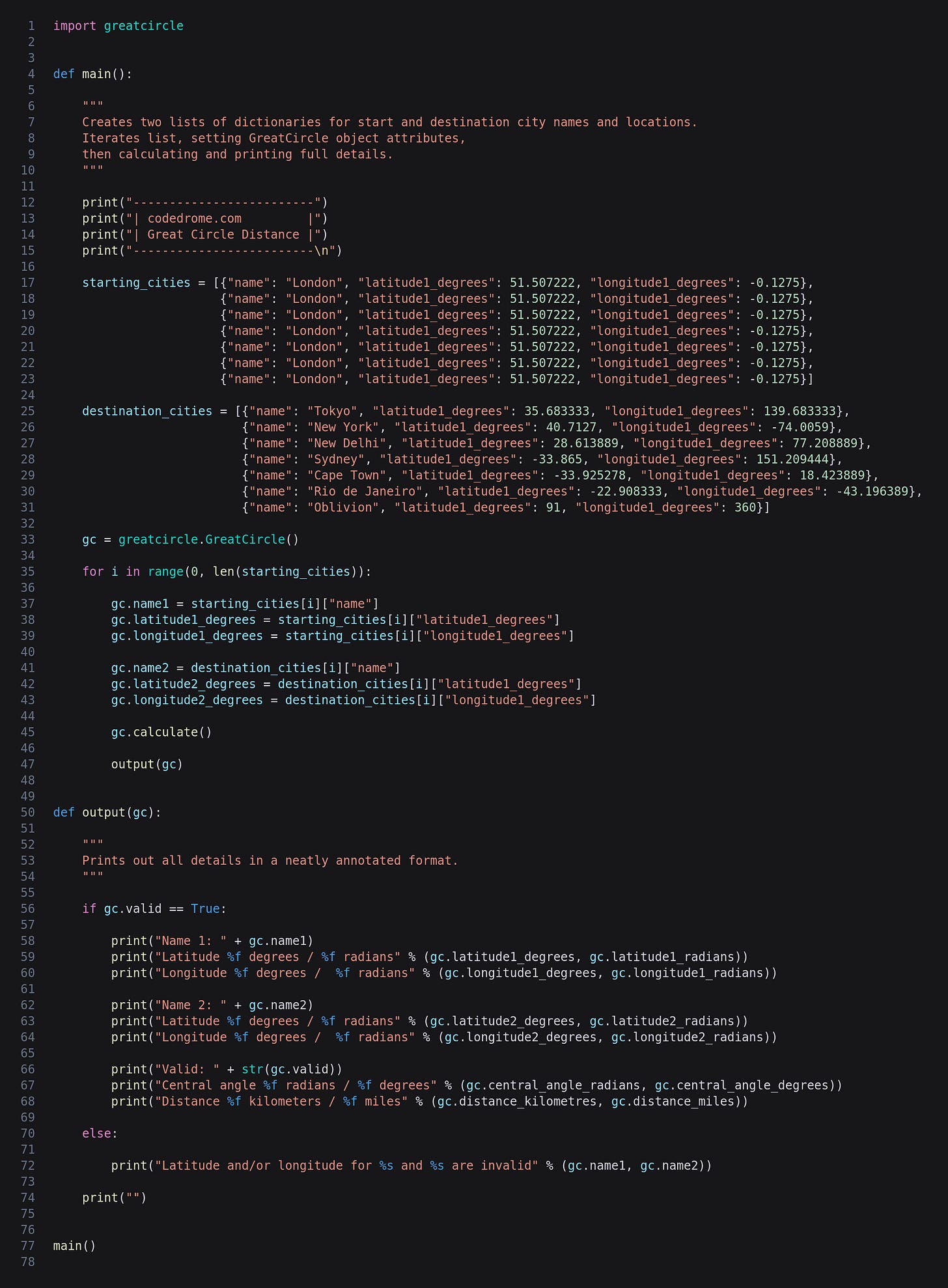
The class is now finished so let's write a bit of code in greatcircledemo.py to try it out.
In the main function I have created two lists of dictionaries representing cities along with their latitudes and longitudes. The last set of values includes the invalid 91° north just to see what happens...!
We then create a GreatCircle object and iterate the lists, setting the object's properties from the current dictionary values before calling calculate. Finally we call the output function which simply prints out the various properties of the object, or a message if the latitude or longitude are invalid.
The code is now finished so we can run it with the following command:
python3 main.py
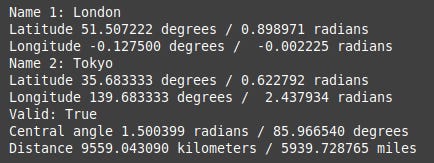
This is the output - I have just shown the first pair of cities here for brevity.
As well as the names, latitudes and longitudes we supplied we now have the latitudes and longitudes in radians, the central angle in both degrees and radians, and the distance in kilometres and miles.