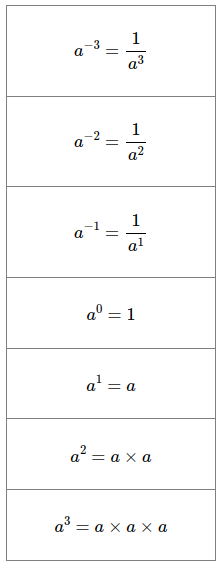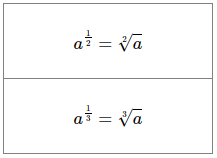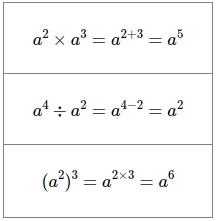Exploring Exponential Powers with Python

Most people are probably familiar with raising numbers to the power of 2 or 3, for example 52 = 5 ✕ 5 = 25 and 43 = 4 ✕ 4 ✕ 4 = 64. You can raise a number to any exponent* although in many cases the meaning isn't obvious. Of course the number of possible exponents is infinite so I won't attempt to cover them all but in this article I'll look at and explain a few of the more useful ones.
Power, exponent and index are pretty much interchangeable. The title of this article is therefore a tautology chosen to keep search engines happy. Sorry!
Integer Exponents
The table below illustrates integer powers from -3 to 3. Negative exponents are the reciprocal (ie division with 1 as the numerator) of the number to the positive power. A number to the power of 0 is always 1, and a number to the power of 1 is just the itself. These might seem useless but it's sometimes helpful to clarify certain expressions such as polynomial equations or, in calculus, the derivatives of certain equations. The last two rows of the table show the familiar square and cube exponents, a2 and a3.
Fractional Exponents
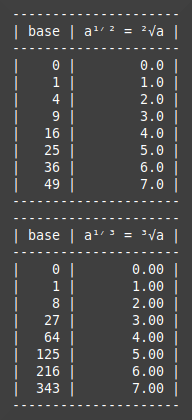
As you can see exponents in the form 1/n are the nth roots. Again using this form can simplify some equations and make them easier to rearrange or otherwise manipulate.
Arithmetic with Exponents
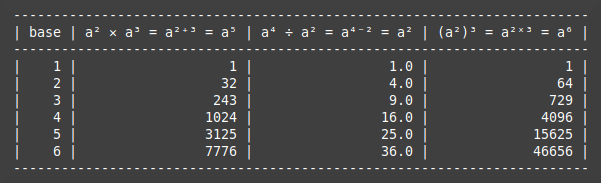
The final three examples show examples of multiplying and dividing exponential terms, including where a term is in brackets. These illustrate that such expressions can easily be simplified.
The Project
This project is very simple and just illustrates the various exponents described above with a range of bases, the numbers raised to a power. You can easily extend it to other bases and/or exponents if you wish to explore the topic further. The code consists of a single Python file called powers.py which you can clone or download from the GitHub repository.
The code for this project use the NumPy library. If you are not familiar with NumPy I have put together a brief introductory guide to get you started.
The Code
This is the full listing for powers.py.
import numpy as np
def main():
print("----------------------------------")
print("| codedrome.com |")
print("| Exponential Powers with Python |")
print("----------------------------------\n")
integers()
# fractions()
# arithmetic()
def integers():
'''
Calculate and print a range of numbers
and those numbers to the power of -3 to 3
'''
start = -6.0
end = 7.0
bases = np.arange(start, end, 1)
pow_minus_3 = np.where(bases!=0, bases, np.NaN)**-3
pow_minus_2 = np.where(bases!=0, bases, np.NaN)**-2
pow_minus_1 = np.where(bases!=0, bases, np.NaN)**-1
pow_0 = bases**0
pow_1 = bases**1
pow_2 = bases**2
pow_3 = bases**3
heading = "| base | a⁻³ = 1/a³ | a⁻² = 1/a² | a⁻¹ = 1/a¹ | a⁰ = 1 | a¹ = a | a = a² ✕ a | a³ = a ✕ a ✕ a |"
print("-" * len(heading))
print(heading)
print("-" * len(heading))
for i in range(0, bases.size):
print(f"| {bases[i]:>4} |", end="")
print(f" {pow_minus_3[i]:>10.4f} |", end="")
print(f" {pow_minus_2[i]:>10.4f} |", end="")
print(f" {pow_minus_1[i]:>10.4f} |", end="")
print(f" {pow_0[i]:>6} |", end="")
print(f" {pow_1[i]:>6} |", end="")
print(f" {pow_2[i]:>10} |", end="")
print(f" {pow_3[i]:>14} |")
print("-" * len(heading))
def fractions():
'''
Various numbers to the power of 1/2 , ie square root,
and 1/3, ie cube root.
'''
squares = np.array([0,1,4,9,16,25,36,49])
squareroots = squares**(1/2)
# The superscript / is Unicode 5151 (decimal) 141F (hexadecimal)
# It is intended for use in for some indiginous Canadian languages
# but I have borrowed it as there is no Unicode superscript /
heading = "| base | a¹ᐟ² = ²√a |"
print("-" * len(heading))
print(heading)
print("-" * len(heading))
for i in range(0,squares.size):
print(f"| {squares[i]:>4} | {squareroots[i]:>10} |")
print("-" * len(heading))
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
cubes = np.array([0,1,8,27,64,125,216,343])
cuberoots = cubes**(1/3)
heading = "| base | a¹ᐟ³ = ³√a |"
print("-" * len(heading))
print(heading)
print("-" * len(heading))
for i in range(0,cubes.size):
print(f"| {cubes[i]:>4} | {cuberoots[i]:10.2f} |")
print("-" * len(heading))
def arithmetic():
'''
Demonstrates a few arithmetic operations with powers:
a² ✕ a³ = a²⁺³
a⁴ ÷ a² = a⁴⁻²
(a²)³ = a²ˣ³
'''
bases = np.arange(1,7,1)
mul = bases**2 * bases**3
div = bases**4 / bases**2
brackets = (bases**2)**3
heading = "| base | a² ✕ a³ = a²⁺³ = a⁵ | a⁴ ÷ a² = a⁴⁻² = a² | (a²)³ = a²ˣ³ = a⁶ "
print("-" * len(heading))
print(heading)
print("-" * len(heading))
for i in range(0,bases.size):
print(f"| {bases[i]:>4} |", end="")
print(f" {mul[i]:>19} |", end="")
print(f" {div[i]:>19} |", end="")
print(f" {brackets[i]:>17} |")
print("-" * len(heading))
if __name__ == "__main__":
main()main
The main function contains three function calls which you can uncomment as and when you want to try out each one.
integers
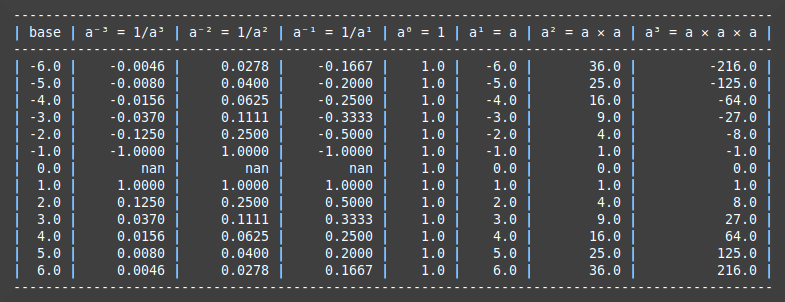
This function creates a range of bases from -6 to 6 and raises them to the powers of -3 to 3. The actual calculations can each be done in a single line as we are using NumPy but there's a slight complication with the negative exponents when the base is 0. For example 0-3 resolves to 1/0, the dreaded "divide by zero" which is mathematically undefined. Straight Python will raise ZeroDivisionError but NumPy just raises a warning. It's still an ugly situation though so I have decided to eradicate it completely by filtering out the 0 base for negative powers. The whole process can still be done in one line, albeit a rather convoluted one, for example:
pow_minus_3 = np.where(bases!=0, bases, np.NaN)**-3
The NumPy where method returns an array containing the values from bases which are not 0, and NaN (not a number) if the value is 0, the whole array then being raised to the relevant power. Dividing NaN by 0 will simply result in another NaN without raising a warning, a much neater solution.
The rest of the function is a bit tedious and messy but just prints out a heading and then iterates and prints the numbers. Run the program like this:
python3 powers.py
which will give you these results. Remember you can edit the code for different bases and/or exponents if you don't mind the fiddly editing of the output code. (As an alternative you could just print the NumPy arrays and forego the nice tabular format.)
fractions
Next we have fractional powers, specifically one half and one third which are equivalent to square and cube roots respectively.
The code for these is similar to that in the integer function but I have hard-coded bases which give nice round integers as roots, and we don't have the zero base problem to deal with. If you uncomment fractions in main you'll get this output.
arithmetic
Lastly comes the arithmetic function which in essence shows how to simplify expressions with exponential terms. I don't think these are at all obvious and if you agree you might like to convince yourself they work with a pen and paper. The general pattern of the code is similar to the previous functions: an array of bases, carry out the exponentiation in one-liners, then print a heading and the results which look like this: