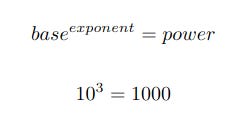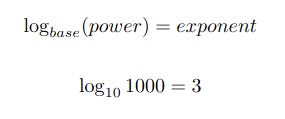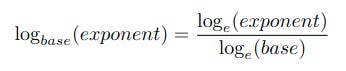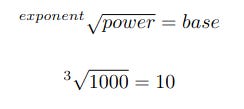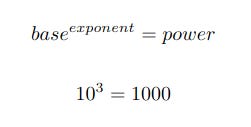Exponents, Logarithms and Roots in Python

In this article I will explore the relationship between bases, exponents and powers, explain some alternative terminology which might lead to confusion, and of course write a bit of Python to demonstrate the concepts.
power from base and exponent
The following illustrates the three entities dealt with by this article, bases, exponents and powers, and the calculation of powers.
You are probably very familiar with this already, and are aware that for example 103 means 10✕10✕10. Take note of the terminology though: the number 10 in this example is the base, the number 3 is the exponent and the result 1000 is the power. The point of this article is to show that if you know any two of these values then you can easily work out the third.
exponent from base and power
The following shows how to use the base and power to calculate the exponent using the log function.
Python provides us with several log functions including one called simply log (specifically math.log) which by default returns the logarithm to base e* but takes an optional argument of any base. I have used math.log in the code but note that Python also provides log2 and log10 which should be used if you know you need these specific bases as they provide more accurate results.
* I will cover e in a separate article.
The log function's ability to use any base is useful but is an opaque "black box" so you might like to know that the process is actually simple, as illustrated by this formula.
As Python already does this there's no practical purpose in writing code to do it but I have written a short function just for anyone interested in the process.
base from exponent and power
The final calculation of the three is to calculate the base from an exponent and a power. This is basically taking the nth root where n is the exponent.
Causes of Confusion
Each of the above set of three calculations is simple and familiar to most people. However, there are several potential points of confusion due to the terminology involved so I'll run through these one at a time.
exponent and power: these words are often used interchangeably but note that they are two different things. Just to make things clear I'll repeat the first formula from above.
logarithm and exponent: two very different words but with the same meaning. Remember that the log functions return exponents.
bases and roots: again two different terms for the same thing, and another thing to learn, remember and understand.
The Project
This project consists of a single file called elr.py which you can clone or download from the GitHub repository.
The Code
This is the code in its entirety.
elr.py
import math
import random
def main():
print("-----------------------------------")
print("| codedrome.com |")
print("| Exponents, Logarithms and Roots |")
print("-----------------------------------\n")
random.seed()
# set base and exponent
# uncomment whichever of these three lines is required
base, exponent = 10.0, 3.0
# base, exponent = 9.0, 2.6
# base, exponent = random.randrange(2, 9), random.randrange(2, 4)
# calculate power
power = base**exponent
print(f"calculate power\n{base:0.2f}^{exponent:0.2f} = {power:0.2f}\n")
# use existing base and power values
# to calculate exponent
# using a logarithm function
exponent = math.log(power, base)
# OR
# exponent = log_base(power, base)
print(f"calculate exponent\nlog{base:0.2f} {power:0.2f} = {exponent:0.2f}\n")
# use existing power and exponent values
# to calculate base or nth root.
base = power**(1.0/exponent)
print(f"calculate base\n{exponent:0.2f}√{power:0.2f} = {base:0.2f}\n")
def log_base(power:float, base:float):
'''
This function duplicates the functionality
of math.log(x, base) to demonstrate using
the default base of e to calculate a logarithm
to another base.
'''
return math.log(power) / math.log(base)
if __name__ == "__main__":
main()At the top of the file math and random are imported, and note the call to random.seed() at the beginning of main to initialize the pseudo-random number generator with the system time.
The first chunk of code implements the first of the three calculations described above, calculating a power from a base and an exponent. There are three different lines of code initializing the known variables and these can be commented/uncommented to use. The first uses the values 10 and 3 from the example, the second uses a couple more numbers, and the third uses random values. The next two lines carry out the calculation and print the entire equation.
Next we calculate and print the exponent from the already-existing power and base values. If you want you can comment/uncomment the code carrying out the calculations to use my homemade log_base function.
Lastly we work out the base. Calculating the nth root of a number is equivalent to raising it to the reciprocal of n, ie 1/n, which is what I typically do in code.
Running the Program
Run the program with this command.
python3 elr.py
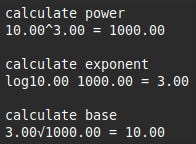
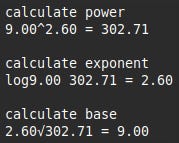
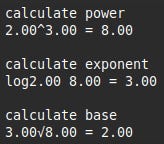
These are the end results using each of the three initial base and exponent values.
As you can see the first replicates the examples above as accurately as it is possible to do in a text-based terminal.
A few strange values here which at least show that you can throw any numbers at the formulae and get back something meaningful.
This is the example using random numbers so yours will almost certainly be different.
The mathematics in this article is pretty simple but I hope both the examples and code have helped you view the three types of calculation as a cohesive whole.
No AI was used in the creation of the code, text or images in this article.