Formula Triangles in Python Part 1
The Inner Workings of the Universe With Just Three Numbers
It's easy to believe that calculations required in the fields of science, technology and engineering are fiendishly complicated and arcane, incomprehensible to all but an elite few. While this can be true you can get a long way by just measuring two values and using simple arithmetic to calculate a third. In this article I'll describe the principles behind these "number triplets" before looking at a few examples.
Just Three Numbers?
I'll start with a simple and easy to understand example of a journey. Three pieces of data we might have or need to calculate about any journey are speed, distance and time. Given any two of these you can calculate the third, the actual arithmetic involved being reasonably obvious and no more than a single multiplication or division. These are the three combinations.
If you know the speed and time you can calculate the distance by multiplying the speed by the time
If you know the distance and time you can calculate the speed by dividing distance by time
If you know the distance and speed you can calculate the time by dividing distance by speed
That's pretty wordy and awkward to use so let's simplify it considerably by using single letters for the three values, and arranging them in a formula triangle which illustrates the arithmetic. It's also necessary to specify the units, and all the formula triangles in this article use SI units which I'll discuss in the next section.
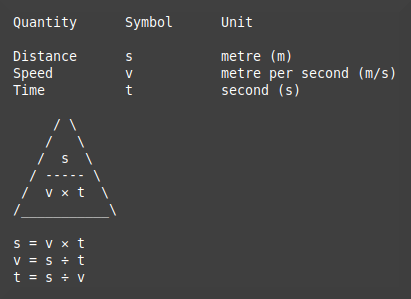
These are the letters and units for the three pieces of journey data.
s - distance travelled in metres
v - speed in metres/second (m/s)
t - time taken in seconds
Letters used by convention aren't always intuitive and can sometimes be confusing. In this case remember s is distance not speed.
This is a formula triangle using the three letters and also illustrating the arithmetic for calculating any of the three quantities from the other two.
To find the formula for calculating a value cover the one you want with your thumb (or other convenient body part) and just read off the remaining formula. If the unknown quantity is at the top then the known values are multiplied, and if the unknown quantity is one of those along the bottom then the known values are divided.
If you do the thumb thing for each of the three values you'll get:
s = v ✕ t
v = s ÷ t
t = s ÷ v
These are simply the calculations described above in words but expressed in much more concise mathematical notation.
It's worth spending a bit of time verifying that the three formulas are actually equivalent. Starting with the first, s = v ✕ t, this shows how it can be rearranged into the second, v = s ÷ t.
s = v ✕ t
swap round so that v is on the left where we want it
v ✕ t = s
divide each side by t
v ✕ t ÷ t = s ÷ t
remove the multiplication and division on the left as they cancel out
v = s ÷ tNow let's rearrange s = v ✕ t into t = s ÷ v.
s = v ✕ t
swap round so that t is on the left where we want it
v ✕ t = s
reverse t and v (not strictly necessary but makes things clearer)
t ✕ v = s
divide both sides by v
t ✕ v ÷ v = s ÷ v
remove the multiplication and division on the left as they cancel out
t = s ÷ vSI Units
I mentioned above that all the examples in this article use SI units. SI stands for Système International, and is referred to as the International System of Units in English. This is a cohesive system of units for measuring a huge range of quantities such as time, distance, speed, and many more. The units may be inconvenient in many circumstances, for example if you are making a journey by car, train or plane you wouldn't use metres, seconds and metres/second to describe it. It is possible to use multiples or fractions in formulas, for example kilometres or millimetres, but doing so can be fiddly or confusing. As a rule I'd recommend converting values to SI units (for example multiplying kilometres by 1000 to get metres) for calculations. You can always convert the result to a more manageable unit afterwards, eg. divide seconds by 3600 to get hours.
Show Me the Python
This project consists of two Python files. The first, formulatriangle.py, contains functions to print out a formula triangle and its associated formulas to the console, and to calculate a missing value from the other two. The second file, formulatriangledemo_1.py, puts the above functions to use with the distance/speed/time example described above. In Part 2 I'll show a few more examples.
The files live in a Github repository so you can download or clone them.
This is the code from formulatriangle.py.
formulatriangle.py
import math
from collections import namedtuple
Quantity = namedtuple("Quantity", "name, symbol, unit, unitabbr")
def output(t, l, r):
'''
Print details of the top, left and right Quantity arguments.
Print a formula triangle using Quantity arguments
Print the 3 individual formulas
'''
print("Quantity Symbol Unit\n")
print(f"{t.name:<14}{t.symbol:<12}{t.unit} ({t.unitabbr})")
print(f"{l.name:<14}{l.symbol:<12}{l.unit} ({l.unitabbr})")
print(f"{r.name:<14}{r.symbol:<12}{r.unit} ({r.unitabbr})")
print(f"\n / \\")
print(f" / \\")
print(f" / {t.symbol} \\")
print(f" / ----- \\")
print(f" / {l.symbol} undefined {r.symbol} \\")
print(f"/___________\\\n")
print(f"{t.symbol} = {l.symbol} undefined {r.symbol}")
print(f"{l.symbol} = {t.symbol} undefined {r.symbol}")
print(f"{r.symbol} = {t.symbol} undefined {l.symbol}")
def evaluate(t: float, l: float, r: float) -> float:
'''
Calculate the missing "not a number"
value from the two supplied values.
Returns nan if arguments invalid.
'''
if math.isnan(t):
return l * r
elif math.isnan(l):
return t / r
elif math.isnan(r):
return t / l
else:
return float('nan')imports
I've imported math for the isnan function, and also namedtuple from collections, which I'll describe next.
The Quantity Named Tuple
The namedtuple is a useful data structure which I use quite regularly but which doesn't seem to have caught on in a big way. It allows you to create a custom tuple type with named properties which allow it to be used a bit like a dictionary.
The syntax for creating one is a bit clumsy IMHO, but once you get used to it it's quite straightforward. Here I've created one called Quantity with four properties:
name, eg distance, speed or timeand support my work
symbol, eg s, v or t
unit, eg metre, metres/second or second
unitabbr, unit abbreviation, eg m, m/s or s
The Quantity tuples are created in calling code so you'll see some examples later.
The output Function
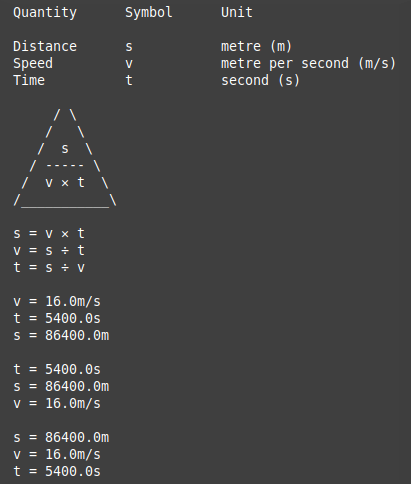
The arguments for this function are three Quantity tuples which it uses to produce output such as this.
Firstly the various bits of each Quantity are printed as a table, then again in a triangle like in the blackboard graphic above, and then again to demonstrate the three individual formulas. This code is very mundane, but note the syntax for referencing named tuple properties:
t.name
t.symbol
t.unit
t.unitabbr I hope you'll agree that this is far easier to use and read than anonymous indexes.
The evaluate Function
This function has three parameters (all floats) but is intended to be used with two only, the missing argument being passed as math.isnan ("not a number"). The code figures out which argument is math.isnan and calculates its value from the other two.
First Example: a Journey
So as not to make this article too long I'll just show one example for the time being, the distance/speed/time calculations from above. In Part 2 I'll present a few more examples.
The example is in formulatriangledemo_1.py.
formulatriangledemo_1.py
import formulatriangle as ft
def main():
print("---------------------")
print("| codedrome.com |")
print("| Formula Triangles |")
print("---------------------\n")
distance_speed_time()
def distance_speed_time():
'''
Calculate the following individual values
relating to a journey from the other two:
* distance
* speed
* time
'''
distance = ft.Quantity("Distance", "s", "metre", "m")
speed = ft.Quantity("Speed", "v", "metre per second", "m/s")
time = ft.Quantity("Time", "t", "second", "s")
ft.output(distance, speed, time)
# set v & t, and calculate s
v = 16.0
t = 5400.0
s = ft.evaluate(float('nan'), v, t)
print()
print(f"v = {v}m/s")
print(f"t = {t}s")
print(f"s = {s}m")
# set s & t, and calculate v
s = 86400.0
t = 5400.0
v = ft.evaluate(s, float('nan'), t)
print()
print(f"t = {t}s")
print(f"s = {s}m")
print(f"v = {v}m/s")
# set s & v, and calculate t
s = 86400.0
v = 16.0
t = ft.evaluate(s, v, float('nan'))
print()
print(f"s = {s}m")
print(f"v = {v}m/s")
print(f"t = {t}s")
if __name__ == "__main__":
main() The core functionality here is in the distance_speed_time function which is called by main. The function first creates three Quantity tuples and passes them to the formula triangle module's output function.
After that there are three chunks of equivalent code which in turn set two of the values and then call evaluate to calculate the third, all three values then being printed. In this and the subsequent examples which I'll show in Part 2 I have used identical values to illustrate the concept of any two values being used to calculate the third.
You can run the program like this:
python3 formulatriangledemo_1.py
This is the output.
You can see that each set of three values is identical, irrespective of which two are known and which one is calculated.
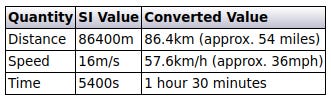
Using the SI system often leads to inconveniently sized values or unfamiliar units. The distance in metres can easily be converted to kilometres by shifting the decimal point three places to the left but it's not so easy to convert seconds or metres per second to familiar quantities. This table should help.
That's all for this instalment but if you want a sneak preview of Part 2 the code is in formulatriangledemo_2.py in the Github repository.