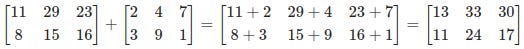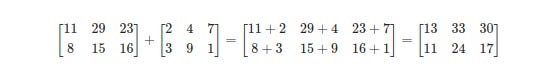Generating TeX for NumPy Matrices with Python

The NumPy library provides an easy and efficient way of creating and using matrices in Python, for example the following code snippet creates two matrices as nothing more than ordinary NumPy arrays and then adds them.
import numpy as np
m1 = np.array([[11,29,23],[8,15,16]])
m2 = np.array([[2,4,7],[3,9,1]])
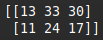
sum = m1 + m2
print(sum) The terminal output looks like this.
For this project I will write Python code which takes NumPy arrays and generates the corresponding TeX matrix notation. As well as individual NumPy matrices I have also included functions to add, subtract and multiply matrices (including scalar arithmetic), each with the option to include intermediate stages.
I am not going to go into any detail about TeX as it is a wide topic and the target audience for this article and its code is those people who are familiar with TeX. If you are not already a TeX user then it is a typesetting format used for mathematical notation so if that's the sort of thing you might find useful I recommend you check it out.
Even if you are a seasoned TeX user you might not be familiar with the notation for matrices so this is an example:
There are several alternatives to bmatrix including pmatrix for round brackets and Bmatrix for curly brackets. When rendered the above TeX displays this:
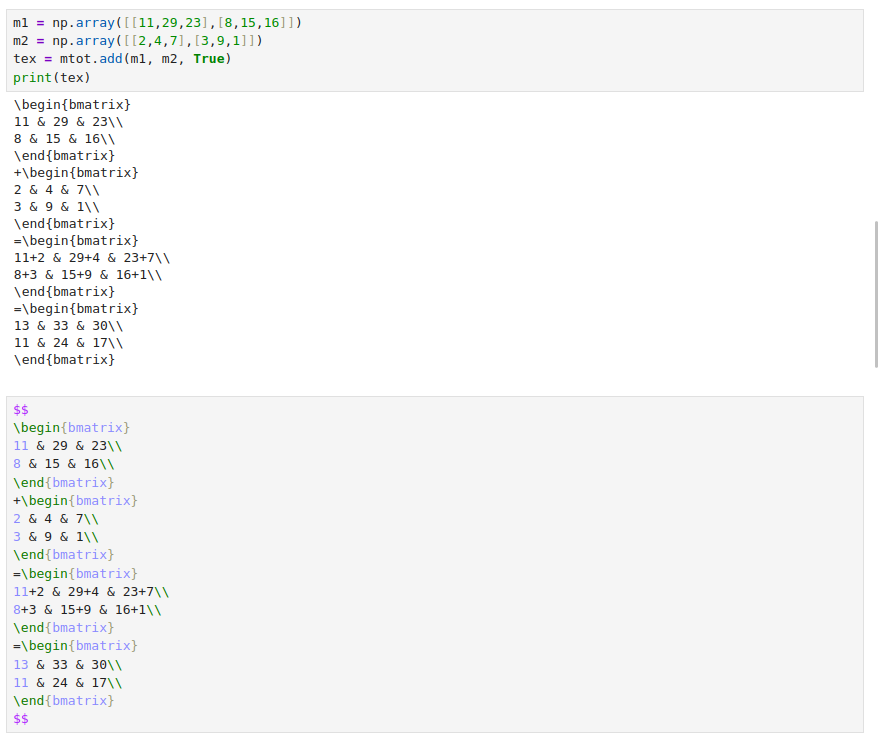
Here is another example of rendered matrices, this time showing addition with the intermediate step. The TeX was generated by this article's code.
The project consists of a Python file, npmatrixtotex.py, which contains a set of functions to generate TeX for the various types of matrix arithmetic. There is also a Jupyter notebook to demonstrate the code in use. I have done this because Jupyter easily renders TeX so after calling the npmatrixtotex functions the output can be pasted into another cell. However, you can use the generated TeX in any way you want.
This project files, npmatrixtotex.py and npmatrixtotex.ipynb, can be cloned or downloaded from the GitHub repository.
No AI was used in the creation of the code, text or images in this article.
The Code
This is the code for npmatrixtotex.py. Don't bother reading it at this stage but just note that it includes the following functions:
matrix (a single matrix)
add
add_scalar
subtract
subtract_scalar
multiply
multiply_scalar
Common "private" functions for the "public" addition and subtraction functions to use. This avoids duplication of near-identical functionality.
Separate "private" functions for the optional intermediate stages.
import numpy as np
'''
This module contains a set of functions to generate TeX
showing arithmetic carried out on matrices represented
by NumPy arrays.
The functions have a show_intermediate parameter
(default false) to show the steps involved
in each operation.
The return values are strings which can be used
in a TeX / LaTeX document between $$ delimiters..
'''
def matrix(m, name:str=None) -> str:
"""
Generates TeX for the NumPy matrix m.
"""
last_col_index = np.shape(m)[1] - 1
tex = []
if name != None:
tex.append(name + "=")
tex.append("\\begin{bmatrix}\n")
for r in m:
for ci, c in enumerate(r):
tex.append(str(c))
if ci < last_col_index:
tex.append(" & ")
tex.append("\\\\\n")
tex.append("\\end{bmatrix}\n")
return "".join(tex)
def add(m1, m2, show_intermediate:bool) -> str:
"""
Generates TeX for the addition of the NumPy
matrices m1 and m2 with optional intermediate step.
"""
return __add_subtract(m1, m2, show_intermediate, np.add, "+")
def add_scalar(m, s, show_intermediate:bool) -> str:
"""
Generates TeX for the addition of the NumPy
matrix m1 and scalar s with optional intermediate step.
"""
return __add_subtract_scalar(m, s, show_intermediate, np.add, "+")
def subtract(m1, m2, show_intermediate:bool) -> str:
"""
Generates TeX for the subtraction of the NumPy
matrices m1 and m2 with optional intermediate step.
"""
return __add_subtract(m1, m2, show_intermediate, np.subtract, "-")
def subtract_scalar(m, s, show_intermediate:bool) -> str:
"""
Generates TeX for the subtraction of the scalar s
from the NumPy matrix m with optional intermediate step.
"""
return __add_subtract_scalar(m, s, show_intermediate, np.subtract, "-")
def multiply(m1, m2, show_intermediate:bool) -> str:
"""
Generates TeX for the multiplication of the NumPy
matrices m1 and m2 with optional intermediate step.
"""
if np.shape(m1)[1] != np.shape(m2)[0]:
raise ValueError("The second matrix must have the same number of rows as the first matrix has columns")
product = m1 @ m2
tex = []
tex.append(matrix(m1))
tex.append(matrix(m2))
tex.append("=")
if show_intermediate == True:
im = __multiply_intermediate(m1, m2)
tex.append(im)
tex.append("=")
tex.append(matrix(product))
return "".join(tex)
def multiply_scalar(m, s, show_intermediate:bool) -> str:
"""
Generates TeX for the multiplication of the NumPy matrix m
by scalar s with optional intermediate step.
"""
product = m * s
tex = []
tex.append(str(s))
tex.append(matrix(m))
tex.append("=")
if show_intermediate == True:
im = __multiply_scalar_intermediate(m, s)
tex.append(im)
tex.append("=")
tex.append(matrix(product))
return "".join(tex)
#~~~~~~~~~~~~~~~~~~~~~~~~~~
# pseudo-private functions
#~~~~~~~~~~~~~~~~~~~~~~~~~~
def __add_subtract(m1, m2, show_intermediate:bool, operation, sign:str) -> str:
# common function for addition and subtraction
if np.shape(m1) != np.shape(m2):
raise ValueError("Both matrices must have the same shape")
result = operation(m1, m2)
tex = []
tex.append(matrix(m1))
tex.append(sign)
tex.append(matrix(m2))
tex.append("=")
if show_intermediate == True:
im = __add_subtract_intermediate(m1, m2, sign)
tex.append(im)
tex.append("=")
tex.append(matrix(result))
return "".join(tex)
def __add_subtract_intermediate(m1, m2, sign:str) -> str:
# common function for addition and subtraction intermediate step.
shape = np.shape(m1)
im = np.empty(shape=shape, dtype='U32')
for row in range(shape[0]):
for col in range(shape[1]):
im[row][col] = f"{str(m1[row][col])}{sign}{m2[row][col]}"
return matrix(im)
def __add_subtract_scalar(m, s, show_intermediate:bool, operation, sign:str) -> str:
# common function for addition and subtraction of scalar
result = operation(m, s)
tex = []
tex.append(matrix(m))
tex.append(sign)
tex.append(str(s))
tex.append("=")
if show_intermediate == True:
im = __add_subtract_scalar_intermediate(m, s, sign)
tex.append(im)
tex.append("=")
tex.append(matrix(result))
return "".join(tex)
def __add_subtract_scalar_intermediate(m, s, sign:str) -> str:
# common function for scalar addition and subtraction intermediate step.
shape = np.shape(m)
im = np.empty(shape=shape, dtype='U32')
for row in range(shape[0]):
for col in range(shape[1]):
im[row][col] = f"{str(m[row][col])}{sign}{s}"
return matrix(im)
def __multiply_intermediate(m1, m2) -> str:
# generates TeX for multiplication intermediate step.
calc = []
m1cols = np.shape(m1)[1]
rows = np.shape(m1)[0]
cols = np.shape(m2)[1]
im = np.empty(shape=(rows, cols), dtype='U64')
for row in range(rows):
for col in range(rows):
for i in range(m1cols):
calc.append(str(m1[row][i]))
calc.append("⋅")
calc.append(str(m2[i][col]))
if i < cols:
calc.append("+")
im[row][col] = "".join(calc)
calc.clear()
return matrix(im)
def __multiply_scalar_intermediate(m, s) -> str:
# generates TeX for scalar multiplication intermediate step.
shape = np.shape(m)
im = np.empty(shape=shape, dtype='U32')
for row in range(shape[0]):
for col in range(shape[1]):
im[row][col] = f"{s}⋅{str(m[row][col])}"
return matrix(im)matrix
This function creates TeX for the NumPy array argument, optionally prefixing it with a name and equals sign. The various bits of the TeX are assembled into a list which is finally joined into a string. This is a more efficient method that concatenating existing strings.
The function is quite simple, iterating rows and columns to add the values to the list and & signs for values not at the end of rows. This function is also used by other functions to create individual matrices.
add, add_scalar, subtract and subtract_scalar
The notation for addition and subtraction of matrices, and scalar addition and subtraction, is nearly identical so to avoid duplicating most of the code I have combined each add/subtract pair into single "private" functions which I'll describe below.
multiply
This function firstly validates the shapes of the two matrices because, as you can see from the error message, "The second matrix must have the same number of rows as the first matrix has columns". If valid the matrices are multiplied using the @ operator not the * operator. After that we just add the matrices to the tex list along with an = sign. If the show_intermediate argument is True this step is generated with a separate function, then the product (result of the multiplication) is added and the joined string returned.
multiply_scalar
No validation is needed here as any shape of matrix can be multiplied by a scalar, and note that in this case the * is used. As usual we then assemble the parts of the TeX into the list, join and return it.
That's the public functions described so now let's look at what I generally refer to as "pseudo-private functions", ie. ones prefixed with __ (double underscore) to indicate that they aren't intended to be used by external code.
__add_subtract and __add_subtract_intermediate
The __add_subtract function generates the near-identical TeX for both matrix addition and subtraction. The actual operation to be carried out is passed as an argument and will be either np.add or np.subtract, and the sign will be "+" or "-" respectively. Both matrices must be the same shape so after validation the operation is carried out on the matrices and the TeX assembled in the usual way.
The __add_subtract_intermediate function is called by __add_subtract if required, and iterates rows and columns to create an array illustrating the actual calculations.
__add_subtract_scalar and __add_subtract_scalar_intermediate
These work in a very similar way to the matrix addition/subtraction functions above. The same np.add and np.subtract methods are used as NumPy can figure out whether it's carrying out the operations on two matrices or one matrix and a scalar.
__multiply_intermediate
Matrix multiplication is fiddly and confusing so this function which creates a matrix to illustrate the process is likely to be useful. The screenshot below includes the intermediate step generated by this function.
__multiply_scalar_intermediate
Scalar multiplication is a lot simpler as you can see from this function.
Trying it Out in Jupyter
The Jupyter notebook which comes with the GitHub repository demonstrates all of the public functions in use. I won't describe each as it would be tedious but will just include screenshots of the Add section. Note that before running any further cells it's necessary to run the imports cell.
The shaded cell at the top is the Python which, when run, generates the output in the unshaded cell beneath it. This output has then been pasted into the second shaded cell between $$ delimiters. (Note this must be a Markdown cell, not Code.) When this cell is run its appearance changes to the following rendered TeX.
(Jupyter chooses to show the first value of each row in purple and the rest in black. I’m sure there’s a rational explanation for this! It works fine even if Jupyter presumably thinks the first values are different in some way.)
The Jupyter notebook contains sets of cells for all the functions in npmatrixtotex.py and they all work in the same way: run the code cell, paste the output TeX into the Markdown cell and then run it to render the matrices.
Remember that you don't have to use Jupyter and could, for example, run the npmatrixtotex functions in ordinary Python and then paste the output into your TeX or LaTeX document.