Polar Plots in Python part 1: Turtle Graphics

Drawing polar plots with Python's Turtle Graphics library

What Are Polar Plots?

You may be familiar with plotting functions on a Cartesian Plane, where for every point on the horizontal x-axis you can calculate a corresponding coordinate on the y-axis using a function of the form:

y = f(x)

For example if you plot

y = x²

you will get something like this.

The above was drawn by iterating x from -10 to 10, and for each value of x calculating the corresponding value of y. Each point x,y is then plotted on the graph.

A polar plot works in a very different way and plots functions in the form

r = f(θ)

where r is the radius, or distance from the origin at 0,0, and θ is the angle. (θ is the Greek letter theta, generally used to denote an angle.) The letter f represents a function carrying out a calculation using the value of θ.

To draw a polar plot we therefore need to iterate between two angles (for example 0° to 360°) and calculate the corresponding value of r for each angle. We then plot the point at the current angle from the origin 0,0, at the current distance r from the origin.

The Project

This project consists of a single Python file called polarplots.py which you can clone/download from the Github repository.

This is the first part of the source code.

polarplots.py part 1

import turtle
import math


def main():

    print("--------------------")
    print("| codedrome.com    |")
    print("| Polar Plots with |")
    print("| Turtle Graphics  |")
    print("--------------------\n")

    # Uncomment this line to make drawing
    # a lot faster or change the argument
    # to any value. Default is 10ms.
    #turtle.delay(0)

    draw_axes(200)

    #plot("circle", 120, 0, 360, circle_function)
    #plot("cardioid", 100, 0, 360, cardioid_function)
    #plot("spiral", 100, 0, 3600, spiral_function)
    #plot("rose", 200, 0, 360, rose_function)

    turtle.hideturtle()

    # This stops the window closing after drawing is finished
    turtle.exitonclick()


def draw_axes(radius):

    """
    Draw lines from the origin every
    15 degrees with the angles labelled.
    """

    FONT_SIZE = 8
    FONT = ("Arial", FONT_SIZE, "bold")

    width = radius * 2 + 100
    height = radius * 2 + 100

    turtle.title("Polar Plot")

    turtle.screensize(canvwidth=width, canvheight=height)
    turtle.setup(width=width + 40, height=height + 40)
    turtle.shape("turtle")

    degree_label_radius = radius + 16

    turtle.pencolor(0.0, 0.0, 1.0)

    for degrees in range(0, 360, 15):

        radians = math.radians(degrees)

        turtle.penup()
        turtle.home()

        turtle.pendown()
        turtle.goto(math.cos(radians) * radius, math.sin(radians) * radius)

        turtle.penup()
        turtle.goto(math.cos(radians) * degree_label_radius,
                    math.sin(radians) * degree_label_radius)

        turtle.goto(turtle.position()[0], turtle.position()[1] - FONT_SIZE)

        turtle.pendown()
        turtle.write(str(degrees) + u'\u00B0', align='center', font=FONT)

Firstly we need to import turtle, and also math. The main function first calls draw_axes which I'll get to in a moment, and then there are a few function calls which are commented out for the time being. At the end of main is a call to turtle.hideturtle, and then turtle.exitonclick to prevent the window closing immediately.

The draw_axes function draws a set of lines out from the origin at 15° intervals from 0° to 360°, and also prints the angle at the end of each. In Turtle Graphics the centre of the screen is 0,0 which makes this process a lot simpler.

Before looping from 0° to 360° we need to get a few things set up:

• The height and width are the radius x 2, plus a bit more for a border

• turtle.title sets the window title

• turtle.screensize sets the size of the drawing surface

• turtle.setup set the size of the window

• turtle.shape sets the shape of the turtle itself, which by default is a boring arrow

• degree_label_radius is the distance of the label from the origin, and needs to be a bit further out than the end of the line

• turtle.pencolor takes a tuple of values between 0.0 and 1.0 NOT rgb values of 0 to 255

Lastly comes the loop, iterating from 0° to 360° at 15° intervals. It doesn't actually get to 360° because that would clash with 0°.

Within the loop we need to do the following:

• Calculate the radian equivalent of degrees for use with math.cos and math.sin

• Lift up the pen and go "home", ie. to 0,0, the centre of the drawing surface

• Put the pen down and go out to the end of the line, drawing as we go

• Lift up the pen and go out to the location where the angle is printed

• Move up from the current position by the size (height) of the font

• Put the pen down and write the current angle including the ° symbol

We now have enough code to run:

python3 polarplots.py

You can now sit back and watch the turtle scurrying across your screen drawing these axes:

You can speed things up or slow them down by uncommenting turtle.delay and entering a value different from the default 10ms.

Let's move on to drawing the plot itself.

polarplots.py part 2

def plot(title, radius, start_degrees, end_degrees, function):

    """
    Draw a polar plot with the given radius
    from/to the given angles.

    The plot positions are calculated by
    the supplied function.

    Any function can be used but it must
    have these arguments:
        radians - the current angle
        radius - in pixels
    and return a dictionary with:
        x - coordinate in pixels
        y - coordinate in pixels
    """

    turtle.title(title)

    turtle.pensize(2)
    turtle.pencolor(1.0, 0.0, 0.0)
    turtle.penup()

    for degrees in range(start_degrees, end_degrees + 1):

        radians = math.radians(degrees)

        pos = function(radians, radius)
        turtle.goto(pos["x"], pos["y"])

        turtle.pendown()


def circle_function(radians, radius):

    """
    Calculate the coordinates of the
    edge of the circle at the given angle.
    """

    return {"x": math.cos(radians) * radius,
            "y": math.sin(radians) * radius}

Most of the work that goes into drawing a polar plot is the same whatever the function calculating the radii. I have therefore written a general-purpose plot function which takes a function as one of its parameters.

After a bit of housekeeping setting the title and pen attributes we iterate between the two angles. After calculating the radian equivalent of the angle comes a call to the function supplied as an argument. This must return a dictionary with the x and y coordinates for the given angle and radius, which are then used in a call to turtle.goto. Lastly we call turtle.pendown: this function draws the plot by moving from one position to the next on each iteration.

The circle_function is the first and simplest of the polar plot functions. All it needs to do is calculate the x and y coordinates for the given angle and radius combination and return them as a dictionary.

Uncomment the first call of the plot function in main and run the program again.

You might like to try different values for the radius and angle arguments.

Now for the last three functions.

polarplots.py part 3

def cardioid_function(radians, radius):

    """
    Calculate the distance from the origin
    for the given angle, then calculate
    its coordinates.
    """

    distance = (1 + math.cos(radians)) * radius

    return {"x": math.cos(radians) * distance,
            "y": math.sin(radians) * distance}


def spiral_function(radians, radius):

    """
    Calculate the distance from the origin
    for the given angle, then calculate
    its coordinates.

    a - the rotation of the spiral
    b - distance between lines
    """

    a = 1
    b = 3

    distance = a + b * radians

    return {"x": math.cos(radians) * distance,
            "y": math.sin(radians) * distance}


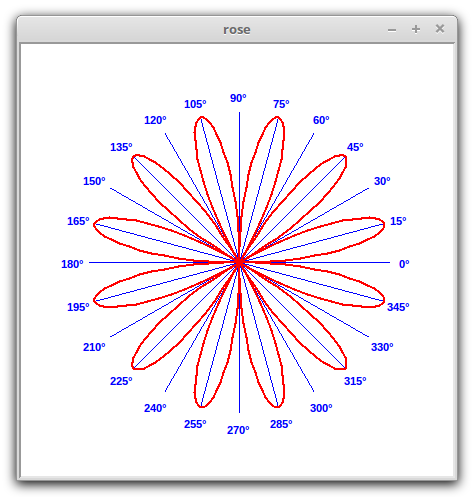
def rose_function(radians, radius):

    """
    Calculate the distance from the origin
    for the given angle, then calculate
    its coordinates.

    I'm not going to tell you what n does!
    Find out for yourself :)
    """

    n = 6

    distance = math.sin(radians * n) * radius

    return {"x": math.cos(radians) * distance,
            "y": math.sin(radians) * distance} 

All the functions take radians and radius arguments, and return a dictionary with the corrrsponding x and y coordinates. You might like to have a go at writing some more - as long as the arguments and return values match you can do anything in the functions themselves.

Uncomment the second, third and fourth calls to plot one at a time and run the program with each in turn. These are the plots.

Again, you might like to try varying the parameters for each function.

The plotting functions shown here are only a few examples but the potential is infinite. If you create any more please feel free to share the code and screenshots on social media.

Turtle graphics is of course not the only way to draw polar plots and as a follow-up to this project I will create a version using Matplotlib.

Please feel free to comment with any thoughts you might have about this article or the code. The project is on Github so you can clone it, enhance it or do anything you like with it. In particular I’d be pleased to see any other polar plot functions you might have discovered or created.