Radians: An Exploration in Python
Measuring and using angles using radians

In my code and articles I often use radians to measure angles. The radian isn't as well known as the degree so to avoid the necessity of describing radians in every article they are used in I have put together this short project to act as a reference to both radians in general and their use in Python. Although this article's primary purpose is as a reference I hope you find it interesting and useful in its own right.
Radians
Everyone gains an understanding of degrees when they are given their first school protractor. The degree is ubiquitous, used in everything from school geometry to navigation and surveying. However, dividing a right angle into 90 units and a full circle into 360 units is entirely arbitrary, originating with the ancient Mesopotamian civilization (centred around the present day Iraq) several thousand years ago.
A more natural unit of angle is the radian which is illustrated by the following diagram.
Starting at the centre point of a circle, draw a line to the edge of the circle. This is the horizontal orange line, and its length is the radius r of the circle. Now draw another line round the edge of the circle the same length r as the first line, and then a third line back to the centre. The angle between the two lines is 1 radian. This angle is always the same irrespective of the size of the circle or the units used to measure it. This is what I mean when I say the radian is a natural unit of angle.
The diagram shows the angles in radians round a full circle, using the standard rad notation. Radians can be defined in terms of π (pi, the ratio of a circle's radius to half its circumference), which means that if we run half way round a circle we are moving through 1π radians. If we keep going back to the start then we have moved through 2π radians. Unlike with degrees, right angles, straight lines and full circles do not contain a nice round number of radians. In fact, as π is an irrational number (ie not an exact fraction so that its digits never end) right angles, straight lines and full circles are all irrational numbers of radians.
Fortunately this isn't a problem as even the modest number of decimal points in Python's math.pi, 3.141592653589793 (15dp), is a perfectly adequate approximation for any practical purpose.
The Project
This project consists of a single Python file, radians.py, which you can clone or download from the Github repository.
The code consists of six functions to demonstrate various aspects of using radians in Python.
pi_conversions: calculate and use the radian/degree conversion factor using π
math_conversion: use Python's built-in conversion functions
degrees_and_radians: print a list of degrees and their radian equivalents
radians_and_degrees: print a list of radians and their degree equivalents
sin_cos_tan: use three of Python's trigonometric functions with radians
asin_acos_atan: three of Python's trigonometric functions
The Code
This is the source code in radians.py.
import math
import numpy as np
def main():
print("-----------------")
print("| codedrome.com |")
print("| Radians |")
print("-----------------\n")
pi_conversions()
# math_conversion()
# degrees_and_radians()
# radians_and_degrees()
# sin_cos_tan()
# asin_acos_atan()
def pi_conversions():
'''
Calculate the number of degrees
in 1 radian using pi and use the
result to convert between the two units.
'''
print("conversions using pi\n--------------------\n")
# as pi is irrational this can only ever be an approximation
d_in_r = 180.0 / math.pi
print(f"degrees in radian:\n180/π = {d_in_r}\n")
d = 90
r = d / d_in_r
print(f"{d}° = {r}rad\n")
r = 1
d = r * d_in_r
print(f"{r}rad = {d}°\n")
def math_conversion():
'''
Use the radians and degrees methods
provided by Python's math module
'''
print("conversions using math\n----------------------\n")
d = 90
r = math.radians(d)
print(f"{d}° = {r}rad\n")
r = 1
d = math.degrees(r)
print(f"{r}rad = {d}°\n")
def degrees_and_radians():
'''
Create and print a list of degrees
and their radian equivalents.
'''
print("degrees and radians\n-------------------")
degrees = np.arange(0,370,10)
radians = np.radians(degrees)
for i, d in enumerate(degrees):
print(f"{d:>4.0f}° = {radians[i]:5.5f}rad")
def radians_and_degrees():
'''
Create and print a list of radians
and their degree equivalents.
'''
print("radians and degrees\n-------------------")
radians = np.arange(0.0, 6.6, 0.2)
degrees = np.degrees(radians)
for i, r in enumerate(radians):
print(f"{r:>4.1f}rad = {degrees[i]:>6.5f}°")
def sin_cos_tan():
'''
Demonstrate the use the sin, cos and tan
with degrees which is WRONG
and radians which is CORRECT.
'''
degrees = 30.0
print(f"degrees = {degrees}\n")
print(f"math.sin(degrees) = {math.sin(degrees):0.3f} *** WRONG ***")
print(f"math.sin(math.radians(degrees)) = {math.sin(math.radians(degrees)):0.3f} *** CORRECT ***\n")
print(f"math.cos(degrees) = {math.cos(degrees):0.3f} *** WRONG ***")
print(f"math.cos(math.radians(degrees)) = {math.cos(math.radians(degrees)):0.3f} *** CORRECT ***\n")
print(f"math.tan(degrees) = {math.tan(degrees):0.3f} *** WRONG ***")
print(f"math.tan(math.radians(degrees)) = {math.tan(math.radians(degrees)):0.3f} *** CORRECT ***\n")
def asin_acos_atan():
'''
Demonstrate the use the asin, acos and atan
with degrees which is WRONG
and radians which is CORRECT.
'''
sin = 0.5
cos = 0.8660254037844387
tan = 0.5773502691896257
print(f"sin = {sin}")
print(f"math.asin(sin) = {math.asin(sin):0.3f}° *** WRONG ***")
print(f"math.degrees(math.asin(sin)) = {math.degrees(math.asin(sin)):0.3f}° *** CORRECT ***\n")
print(f"cos = {cos}")
print(f"math.acos(cos) = {math.acos(cos):0.3f}° *** WRONG ***")
print(f"math.degrees(math.acos(cos)) = {math.degrees(math.acos(cos)):0.3f}° *** CORRECT ***\n")
print(f"tan = {tan}")
print(f"math.atan(tan) = {math.atan(tan):0.3f}° *** WRONG ***")
print(f"math.degrees(math.atan(tan)) = {math.degrees(math.atan(tan)):0.3f}° *** CORRECT ***\n")
if __name__ == "__main__":
main()import & main
At the top of the file we import math and numpy. The math module is a Python built-in but NumPy is an external library which needs to be installed with
pip install numpy
if you haven't already. This is its PyPI page.
The main function just contains calls to the various other functions in the file which can be uncommented as and when you want to run them.
pi_conversions
As you can see from the diagram above 180° = 1πrad so the conversion factor between degrees and radians is 180/π = 57.29577951308232, the number of degrees in a radian to 14dp.
This function carries out the above calculation and then uses it to convert 90° to radians, and 1rad to degrees. Note that this is just to illustrate the mathematics involved and is not the best way to carry out the conversions.
Run the program with this command.
python3 radians.py
This is the output.
math_conversion
Python's math module provides us with two functions for converting between radians and degrees called, rather unimaginatively, radians and degrees. This function uses them to carry out the same conversions as in the previous function. Uncomment math_conversion in main and run the program again.
The results are identical. Phew!
degrees_and_radians & radians_and_degrees
The lists of radian and degree equivalents created by these functions may help gain an intuitive sense for the relative values but the main purpose is to demonstrate the NumPy radians and degrees methods.
The functions create arrays of numbers using the arange method, the arguments being start and end points and intervals. A core feature of NumPy is the ability to call a function on an entire array with one statement rather than using a loop, and in this case calling the radians and degrees methods with the arrays created with arange returns arrays of converted values. The original and converted values are then printed in a neat table format.
Uncomment these two function calls in main and run the program.
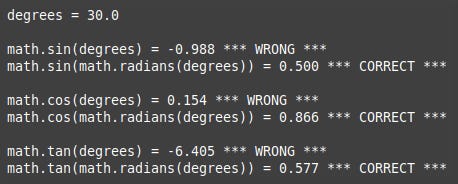
sin_cos_tan
This and the next function demonstrate radians in action with trigonometric functions. If you're a bit rusty on the whole sin, cos and tan stuff this diagram gives a refresher.
For any right-angled triangle ("right triangle" in mathematical speak) the ratios of the lengths of the sides can be calculated if you know one of the other angles. In this case we the angle 30° so calculating the sin (sine) and cos (cosine) of this angle tells us that the opposite and adjacent sides are respectively 0.5 and 0.866 times the length of the hypotenuse, the longest side. As these are ratios the actual units are irrelevant. It works just the same with millimetres and light-years. The third function, tan (tangent) isn't shown on the diagram but gives the ratio of the opposite side to the adjacent side, in this case 0.5/0.866 = 0.577.
That's trigonometry in a nutshell but in Python there's a gotcha, Yes, you guessed it, sin, cos and tan as well as the other related functions take arguments and return values in radians, not degrees. This isn't a problem as it's easy to use the math.radians and math.degrees demonstrated in math_conversion.
The sin_cos_tan function does just that but I have also used degrees just to prove that doing so gives the wrong answers. (Although I'm sure you believed me anyway!)
Uncomment sin_cos_tan(), run the program and note the incorrect and correct answers.
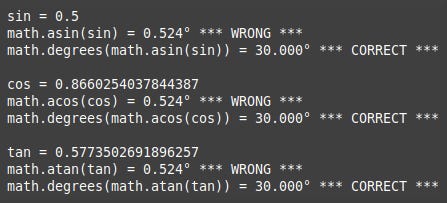
asin_acos_atan
To wrap this project up I'll write another function very similar to the previous, but this time with the asin, acos and atan functions. To give them their full names they are arcsine, arccosine and arctangent and are the inverse of sin, cos and than which means that they take ratios such as 0.5 and return the corresponding angle, in this case 30°. However, the Python asin, acos and atan functions of course return the angles in radians so we need the math.degrees function.
I have used the same sin, cos and tan values from the diagram and sin_cos_tan function, so asin, acos and atan should all give us 30° after conversion. Run asin_acos_atan which gives this output.
Radians in the Real World
If you are writing code that uses angles or are just using trigonometric functions to model cyclical behaviour then it's easy to lose track of which unit a particular variable or data structure uses. I have therefore put together a few suggestions for how to avoid getting in a muddle. I'm not claiming these are "best practice", just a few ideas to adapt to your own requirements and preferences.
If you are in the rare but fortunate situation of only needing radians through the whole input/calculation/output process then naturally you can just use radian variables and forget degrees even exist.
Include the units in variable names, eg. latitude_degrees or angle_A_radians.
Decide on a policy for when you are going to carry out conversions. In a situation where users input angles in degrees and expect output in degrees then my opinion is that conversion should be done at the points of input and output, with all values being stored in radians (including when saved to files or databases). The opposite approach is to store everything in degrees and do radian conversions as and when radians are passed to or returned from functions. Choose one and stick to it.
If you have a lot of calls to sin, cos, tan etc. scattered all over your code base then you might think it worthwhile writing short wrapper functions such as sin_deg(degrees) which call the built-in Python functions but also carry out the necessary conversions.
If you write code which uses angles or trigonometric functions I'd be interested to know how you handle them, and if you have anything to add to the bullet-point suggestions above.