Exploring Radioactive Decay Half-Lives with Python

In this article I will briefly explain radioactive decay and the concept of half-lives, and then go on to write Python code to illustrate the underlying mathematics.
Radioactive Decay and Half-Lives
All atoms of a particular chemical element have a fixed number of protons in their nuclei, and this is what defines an atom as being of a particular element. However, nuclei can also contain varying numbers of neutrons, and each combination of proton and neutron numbers is called a nuclide.
Some of these nuclides are unstable and therefore radioactive, and are known as radionuclides. There are 339 naturally occurring nuclides on earth (many more have been created in particle accelerators or nuclear reactors) of which 252 are believed to be stable as no decay has ever been observed. The other 87 are unstable of which 34 are primordial radionuclides, the rest being created by the decay of primordial radionuclides as part of a so-called decay chain.
The decay of an individual atom of a radioactive nuclide is random and unpredictable. However, the time for which the probability of an atom decaying is 0.5 can be established by measuring a sufficiently large sample of the nuclide; this time is known as the nuclide's half-life.
Given a reasonable sample size, the nuclide will decay by approximately 50% during its half-life. The remaining amount of the nuclide will decay by approx. 50% during the next half-life, leaving 25% of the original amount and so on.
This graph shows the amount remaining across 5 half-lives of a radionuclide. The actual units being measured are not shown as they could be the amount of radiation, or the mass or number of atoms of the nuclide remaining.
That was a very brief introduction to the concept of the half-life as applied to radioactive decay. The main purpose of this article is to examine the mathematical aspects and to demonstrate them with some Python code.
The Project
This project consists of the following files:
radioactivenuclides.py
halflifeutilities.py
halflife.py
which you can clone/download the GitHub repository.
The radioactivenuclides.py file contains a dictionary of the 34 primordial radionuclides, including their half-lives.
The halflifeutilities.py file includes functions for the following tasks:
Print the nuclides in radioactivenuclides.py
Calculate the amounts of a radionuclide left across a number of half-lives
Print the above list
Calculate the amount of a radionuclide left after a specified time
Calculate the amount of time taken for a radionuclide to decay to a certain amount
In halflife.py we have a main function which calls the functions in the previous file.
radioactivenuclides.py
Firstly let's take a look at the data in radioactivenuclides.py; this just shows the first three items.
radioactive_nuclides = {
"tellurium128":
{
"element": "tellurium",
"elementsymbol": "Te",
"atomicmass": 128,
"significand": 2.2,
"exponent": 24
},
"xenon124":
{
"element": "xenon",
"elementsymbol": "Xe",
"atomicmass": 124,
"significand": 1.8,
"exponent": 22
},
"krypton78":
{
"element": "krypton",
"elementsymbol": "Kr",
"atomicmass": 78,
"significand": 9.2,
"exponent": 21
}, This file is simply data coded as dictionaries inside a dictionary. As I mentioned it contains the 34 primordial radionuclides but you can add to them if you wish.
The keys to the outer dictionary are the names of the elements concatenated with the nuclide's atomic mass, ie. the total number of protons and neutrons in the nucleus.
The inner dictionaries contain the following data:
element - the element's name
elementsymbol - the 1 or 2 letter element symbol
atomicmass - the the number of protons and neutrons in the nucleus
significand and exponent - the components of the scientific form of the nuclide's half-life in years, for example tellurium 128's half-life is 2.2 x 1024
halflifeutilities.py
This is the halflifeutilities.py file.
from typing import List, Dict
import math
import radioactivenuclides as ran
def _sci_not_to_num(significand, exponent):
return significand * 10 ** exponent
def printnuclides() -> None:
"""
Print details of the the contents of
radioactivenuclides as a table
"""
print("-" * 71)
print("| Key ", end="")
print("| Nuclide symbol ", end="")
print("| Nuclide name ", end="")
print("| Half-life (years) |")
print("-" * 71)
for key, value in ran.radioactive_nuclides.items():
print(f"| {key.ljust(14, ' ')}|", end="")
print(f" {(str(value['atomicmass']) + value['elementsymbol']).ljust(15, ' ')}|", end="")
print(f" {(value['element'] + ' ' + str(value['atomicmass'])).ljust(15, ' ')}|", end="")
print(f" {(str(value['significand']) + 'undefined10^' +str(value['exponent']) ).ljust(18, ' ')}|")
print("-" * 71)
def decay_list(nuclidekey: str, halflives: int, startingvalue: int = 1048576) -> List:
"""
For the specified nuclide creates a list of
amounts remaining after each half-life has elapsed
"""
dl = []
nuclide = ran.radioactive_nuclides[nuclidekey]
halflife = _sci_not_to_num(nuclide['significand'], nuclide['exponent'])
for i in range(0, halflives + 1):
remaining = 0.5**i
dl.append({
"years_elapsed": halflife * i,
"remaining_decimal": remaining,
"remaining_amount": startingvalue * remaining
})
return dl
def decay_table(nuclidekey: str, halflives: int, startingvalue: int = 1048576) -> None:
"""
For specified nuclide prints table of half lives and years,
and amounts remaining as decimals and amounts.
"""
dl = decay_list(nuclidekey, halflives, startingvalue)
tablewidth = 75
nuclide = ran.radioactive_nuclides[nuclidekey]
halflife = _sci_not_to_num(nuclide['significand'], nuclide['exponent'])
print(f" {nuclide['element']} {nuclide['atomicmass']}\n")
print(f" Half-Life {nuclide['significand']}undefined10^{nuclide['exponent']} years\n")
print("-" * tablewidth)
print("| Elapsed | Remaining |")
print("-" * tablewidth)
print("| Half-Lives ", end="")
print("| Years ", end="")
print("| Decimal | Amount |")
print("-" * tablewidth)
for index, item in enumerate(dl):
print(f"| {index:<11d}|", end="")
print(f" {item['years_elapsed']:<17e}|", end="")
print(f" {item['remaining_decimal']:<19.12f} |", end="")
print(f" {item['remaining_amount']:<17.8g} |")
print("-" * tablewidth)
def at_time(nuclidekey: str, years: int, startingvalue: int = 1048576) -> Dict:
"""
Calculates amount of nuclide remaining after
specified number of years.
Result is a dictionary with keys remaining_decimal
and remaining_amount
"""
nuclide = ran.radioactive_nuclides[nuclidekey]
halflife = _sci_not_to_num(nuclide['significand'], nuclide['exponent'])
exponent = -(years / halflife)
remaining_decimal = 2**exponent
remaining_amount = startingvalue * remaining_decimal
return { "remaining_decimal": remaining_decimal, "remaining_amount": remaining_amount }
def time_to(nuclidekey: str, remaining_decimal: float) -> float:
"""
Calculates the amount of time for a nuclide
to decay to the specified proportion
"""
nuclide = ran.radioactive_nuclides[nuclidekey]
halflife = _sci_not_to_num(nuclide['significand'], nuclide['exponent'])
factor = -(math.log2(remaining_decimal))
return halflife * factor _sci_not_to_num
As I just mentioned the half-lives of nuclides in radioactivenuclides.py are stored as significands and exponents of the scientific notation. This function calculates the actual number from these values for use in calculations.
printnuclides
This function simply prints the contents of radioactivenuclides.py in a table format. The "Nuclide symbol" consists of the atomicmass and elementsymbol values concatenated. "Nuclide name" is the concatenation of element and 128 with a space between them.
The half-lives are shown in the format 2.2×10^24. Python uses the format 2.2e+24 which I dislike so I stored half lives as significands and exponents to make output simpler. I could have done things the other way round, storing the actual value and converting to significands and exponents just for output. However, this can generate slightly inaccurate results with decimals such as .000000000001 or .999999999999.
decay_list
The decay_list function takes a nuclide key (as used in the radioactive_nuclides dictionary), a number of half lives and a starting value. It then calculates the fraction remaining after each half-life, adding a dictionary of the number of half-lives elapsed, and the fraction and actual amount left to a list. The startingvalue and remaining_amount can represent radiation, mass or number of atoms.
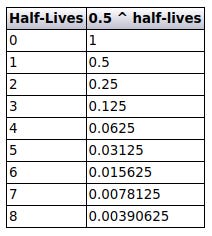
The fraction remaining is calculated by raising 0.5 to the power of the number of half-lives elapsed, which is represented by the loop index. The following table shows how this works.
decay_table
Here we print the data generated by decay_list. After printing the name of the nuclide and its half-life we print some headings and then the data itself within a loop.
at_time
This function takes a nuclide, number of years and a starting value and calculates the remainder (both fraction and amount) after the specified number of years. This table displays an example of the calculation for the arguments shown.
The number of years is 0.5 of the half-life, and if you look at the graph above you can see the curve is at about 0.7 at this point on the x-axis.
time_to
The time_to function takes a nuclide key and a decimal fraction, and calculates how long it takes the radionuclide to decay to that fraction. This is an example of arguments and calculated values.
I chose 0.5 for the value of remaining_decimal to give an obvious result which is the half-life, and as you can see we have reached the correct result.
halflife.py
The halflife.py code is short and simple, and just runs the functions from halflifeutilities.py.
import halflifeutilities as hlu
import radioactivenuclides as ran
def main():
print("-------------------------------------")
print("| codedrome.com |")
print("| Half Life of Radioactive Nuclides |")
print("-------------------------------------\n")
hlu.printnuclides()
# hlu.decay_table("uranium235", 8, 1048576)
# nuclide = ran.radioactive_nuclides["tellurium128"]
# halflife = nuclide['significand'] * 10 ** nuclide['exponent']
# at = hlu.at_time("tellurium128", halflife * 0.5, 1048576)
# print(at)
# tt = hlu.time_to("tellurium128", 0.5)
# print(f"{tt} Years")
# print(f"{tt:,.0f} Years")
# print(f"{tt / 1000000:,.0f} Million Years")
# print(f"{tt / 1000000000:,.0f} Billion Years")
# print(f"{tt / 1000000000000:,.0f} Trillion Years")
if __name__ == "__main__":
main() The first two sections of code simply call functions, the second, decay_table, with your choice of arguments.
For at_time I have first picked up the half life of tellurium 128 and then multiplied it by 0.5 for the years argument, before printing the result.
After calling time_to I have printed the result in no less than 5 formats. The first just prints the result in whatever way Python sees fit, whereas the rest print it in ever-larger multiples of years.
Now we can run the code like this:
python3 halflife.py
This is the output of the printnuclides function. You can see here the scientific notation format I have used.
Program Output: printnuclides
If you comment out printnuclides in main and uncomment decay_table this is the output.
Program Output: decay_table
Uncomment the next 4 lines of code in main which gives us this. Note that the result is returned as a dictionary.
Program Output: at_time
Finally run the last 6 lines of code.
Program Output: time_to
I hope you found this article interesting and useful. I have used radioactive decay to illustrate the concept of exponential decay but the principle has many other applications so it is useful to both understand it and be able to implement it in code.