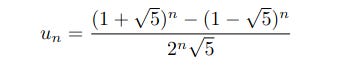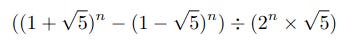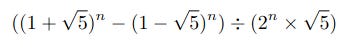The Fibonacci Sequence and Binet's Formula in Python

You can calculate the Fibonacci Sequence by starting with 0 and 1 and adding the previous two numbers, but Binet's Formula can be used to directly calculate any term of the sequence. This short project is an implementation of that formula in Python.
You are probably familiar with the Fibonacci sequence and it's application to the hypothetical breeding habits of rabbits, but you may wish to brush up on the subject by reading the relevant Wikipedia article, as well as the article on Binet and his formula.
Fibonacci number
Jacques Philippe Marie Binet
The formula is:
which can be represented in a way more useful for implementation in a programming language as:
The Code
This project consists of a single file called binetsformula.py which you can clone or download from the Github repository.
import math
def main():
try:
print_fibonacci_to(16)
except ValueError as ve:
print(ve)
def binets_formula(n: int):
"""
The central function implementing
Binet's Formula, returns n-th term.
"""
# pre-calculate sqrt(5) as we use it 3 times
sqrt5 = math.sqrt(5)
# OR
# sqrt5 = 5**0.5
F_n = int((( (1 + sqrt5) ** n - (1 - sqrt5) ** n ) / ( 2 ** n * sqrt5 )))
return F_n
def print_fibonacci_to(n: int):
"""
Prints the Fibonacci Sequence to the given term
using both addition of the previous two terms and
Binet's Formula.
"""
if n < 2:
raise ValueError("n must be >= 2")
else:
F_n_minus_2 = 0
F_n_minus_1 = 1
F_n_seq = 0
F_n_Binet = 0
# print heading and first two hard-coded terms
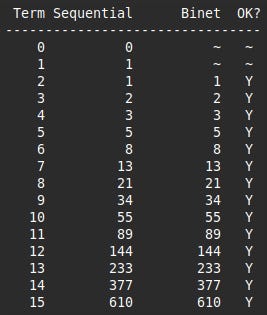
print("\n Term Sequential Binet OK?\n--------------------------------")
print(f" 0 {F_n_minus_2:3d} ~ ~")
print(f" 1 {F_n_minus_1:3d} ~ ~")
for term in range(2, n):
# calculate current term both ways
F_n_seq = F_n_minus_2 + F_n_minus_1
F_n_Binet = binets_formula(term)
print(f"{term:5d} {F_n_seq:10d} {F_n_Binet:10d}", end='')
# Check both are the same!
if(F_n_Binet == F_n_seq):
print(" Y")
else:
print(" N")
# Set previous two terms ready for next iteration
F_n_minus_2 = F_n_minus_1
F_n_minus_1 = F_n_seq
if __name__ == "__main__":
main()After importing math for its sqrt and pow functions the main function simply calls the print_fibonacci_to function which I'll describe further down.
The binets_formula function calculates the value of the Fibonacci Sequence for the given term n. The formula uses √5 no less than three times so I have assigned it to a separate variable, both for efficiency and to make the code slightly more concise.
The next line is Binet's Formula itself, the result of which is assigned to the variable F_n - if you examine it carefully you can see it matches the formula in the form.
Using √5 will force Python to evaluate the formula as a real number so the whole expression is cast to an integer using the int function. Lastly we just need to return F_n.
The print_fibonacci_to function calculates and prints the values of the Fibonacci Sequence up to and including the given term n. It does this in two ways, the conventional way of adding the two previous terms and also using Binet's Formula. It also checks the two match, as they always should.
After checking that n is > 2 we declare variables to hold the previous two terms of the sequence, and the current term as calculated sequentially and using Binet's formula. We then print out some column headings and the first two terms before getting to the main part of the function: a for loop from 2 to the required term.
In this loop we calculate the term firstly by adding the two previous terms, and then by calling the binets_formula function. These are then printed, followed by a Y/N indicator of whether the two are the same - hopefully the "else" will never be used. Lastly we change the variables holding the previous two terms ready for the next iteration.
The code is now finished so enter the following in your terminal to run it.
python3 binetsformula.py
The output is:
No AI was used in the creation of the code, text or images in this article.