Exploring Sound Waves with Python

For this project I will write Python code to demonstrate the relationship between the frequencies and wavelengths of sound waves, and how they behave in mediums such as air and water.
Sound waves consists of varying pressures radiating outwards from the source of the sound. The distance between equal pressures is the wavelength, and as the speed is constant* in a given medium such as air the frequency or number of waves in a specific period of time varies inversely with the wavelength. The closer together the waves are the more you get in a period of time, so wavelength and frequency are two ways to measure the same thing.
* the speed of sound does vary somewhat but I have used approximate average values
The code for this article is based around a class representing a sound wave with a specified wavelength and frequency, with either unspecified property being calculated from the other.
A while ago I wrote a pair of articles on formula triangles:
Formula Triangles in Python Part 1
Formula Triangles in Python Part 2
which are an easy way to represent many formulas used in science and technology where an unknown quantity can be calculated from two others. One of the examples I included was the relationship between the frequency, wavelength and speed of waves. This set of formulas applies to all waves including electromagnetic (light, radio etc.) but in this article I will apply them specifically to sound waves.
As a brief recap here is the formula triangle for the three core properties of waves.
The variables are:
V: velocity (metres per second or m/s)
f: frequency (hertz or Hz, the number of waves per second)
λ (the Greek letter lambda): wavelength (in metres)
To find an unknown value carry out the calculation shown by the two known values, thus:
V = f ✕ λ
f = V ÷ λ
λ = V ÷ f
To illustrate the code in use I'll use four different frequencies:
500Hz - a handy frequency to start with as it has a nice round speed and wavelength values which are easy to calculate by hand
261.63Hz - seems a bit random but is the frequency of middle C
20Hz - the lowest audible to humans* (if you are a whale you can hear lower frequencies)
20000Hz - the highest audible to humans (if you are a dog you can hear higher frequencies)
* this is variable and the upper limit tends to decrease with age
The Code
This project consists of the following files:
soundwave.py
soundwavedemo.py
which you can clone/download from the GitHub repository.
This is soundwave.py.
import math
SPEED_AIR_MS = 330.0
SPEED_WATER_MS = 1500.0
MIDDLE_C_FREQUENCY = 261.63
MIN_HUMAN_FREQUENCY = 20.0
MAX_HUMAN_FREQUENCY = 20_000.0
class SoundWave(object):
'''
An immutable class representing the three
key characteristics of a sound wave:
speed in metres/second (varies according to medium)
wavelength in metres (varies according to medium)
frequency (constant across mediums)
'''
def __init__(self,
speed_ms:float=math.nan,
wavelength_m:float=math.nan,
frequency_hz:float=math.nan):
self._speed_ms = speed_ms
self._wavelength_m = wavelength_m
self._frequency_hz = frequency_hz
self._calc_speed()
self._calc_wavelength()
self._calc_frequency()
def __str__(self) -> str:
str = []
str.append(f"speed {self._speed_ms}m/s\n")
str.append(f"wavelength {self._wavelength_m}m\n")
str.append(f"frequency {self._frequency_hz}Hz")
return "".join(str)
#~~~~~~~~~~~~~~~~~~~~~~~~~~#
# pseudo-private functions #
#~~~~~~~~~~~~~~~~~~~~~~~~~~#
def _calc_wavelength(self) -> None:
# λ = V/f
if math.isnan(self._wavelength_m) and \
not math.isnan(self._frequency_hz) and \
not math.isnan(self._speed_ms):
self._wavelength_m = self._speed_ms / self._frequency_hz
def _calc_frequency(self) -> None:
# f = V/λ
if math.isnan(self._frequency_hz) and \
not math.isnan(self._wavelength_m) and \
not math.isnan(self._speed_ms):
self._frequency_hz = self._speed_ms / self._wavelength_m
def _calc_speed(self) -> None:
# V = fλ
if math.isnan(self._speed_ms) and \
not math.isnan(self._wavelength_m) and \
not math.isnan(self._frequency_hz):
self._speed_ms = self._frequency_hz * self._wavelength_mAt the top of the file are a few constants for speeds and frequencies which will make it easier to try out the class.
Next comes the SoundWave class whose __init__ arguments are speed_ms, wavelength_m and frequency_hz, the three values discussed above. The arguments are used to set properties, and then three functions are called which attempt to set any unknown value.
Note that the code is pretty primitive and intended only to illustrate the speed/wavelength/frequency relationship so there is no validation or other bells and whistles required for robust or production-quality code. If you want to improve this code in any way you are welcome to fork the Github repository.
The __str__ function simply assembles the properties into a user-friendly string.
The three _calc functions check for combinations of one NaN (not a number) and two "not not a number" and calculate the missing value from the other two using the respective formulas shown above.
That's it. Simple but it does the job. Now let's try it out in soundwavedemo.py.
import soundwave as sw
def main():
print("-----------------")
print("| codedrome.com |")
print("| Sound Wave |")
print("-----------------\n")
# set speed and frequency
# SoundWave class calculates wavelength
air = sw.SoundWave(speed_ms=sw.SPEED_AIR_MS, frequency_hz=500.0)
water = sw.SoundWave(speed_ms=sw.SPEED_WATER_MS, frequency_hz=500.0)
print(air)
print()
print(water)
# set speed and wavelength
# SoundWave class calculates frequency
air = sw.SoundWave(speed_ms=sw.SPEED_AIR_MS, wavelength_m=0.66)
water = sw.SoundWave(speed_ms=sw.SPEED_WATER_MS, wavelength_m=3.0)
print("-"*32)
print(air)
print()
print(water)
# set frequency and wavelength
# SoundWave class calculates speed
air = sw.SoundWave(frequency_hz=500.0, wavelength_m=0.66)
water = sw.SoundWave(frequency_hz=500.0, wavelength_m=3.0)
print("-"*32)
print(air)
print()
print(water)
#--------------------------------------------------------------
print("-"*32)
middle_c_air = sw.SoundWave(speed_ms=sw.SPEED_AIR_MS, frequency_hz=sw.MIDDLE_C_FREQUENCY)
print(middle_c_air)
print("-"*32)
min_human_air = sw.SoundWave(speed_ms=sw.SPEED_AIR_MS, frequency_hz=sw.MIN_HUMAN_FREQUENCY)
print(min_human_air)
print("-"*32)
max_human_air = sw.SoundWave(speed_ms=sw.SPEED_AIR_MS, frequency_hz=sw.MAX_HUMAN_FREQUENCY)
print(max_human_air)
print("-"*32)
if __name__ == "__main__":
main()After importing soundwave the first three chunks of code in main set different combinations of two arguments, allowing the SoundWave class to calculate the other. Each correspond to the same wavelength so the outputs will be identical. For each combination I have created two SoundWave objects, one for air and one for water.
The rest of the code creates three more SoundWave objects, all using the speed of sound in air but for middle C and the minimum and maximum human-audible frequencies.
Running the Program
Now we can run the code like this:
python3 soundwavedemo.py
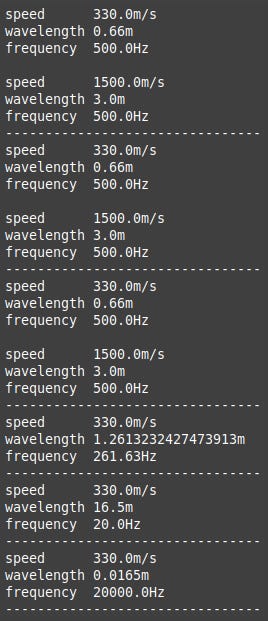
This is the output in its entirety.
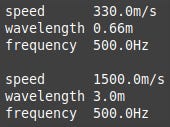
The first three sets of output are identical and look like this . . .
. . . but as you know the values were calculated in three different ways depending on which combinations of properties were set. You were probably aware that the speed of sound in water and thus the wavelength of a particular frequency differs from those in air but you might be surprised at how much.
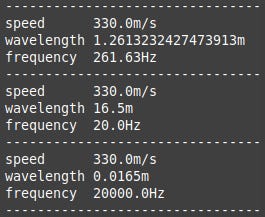
This is the last part of the output and shows middle C and the approximate lowest and highest sounds we can hear.
It would be easy to create a table of frequency/wavelength values, from say 20Hz to 20000Hz in 1000Hz intervals, but that would be boring so as a follow-up I'll plot the values using Matplotlib.
If you have any comments I would be interested to read them, and please subscribe for weekly Python posts on science, mathematics and related topics.
No AI was used in the creation of the code, text or images in this article.