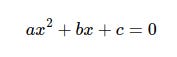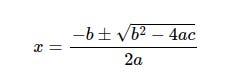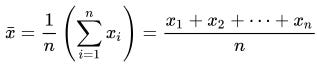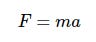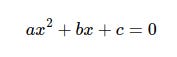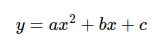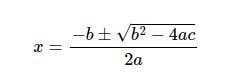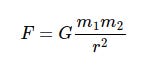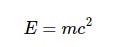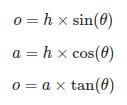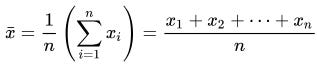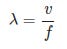Implementing Mathematical Formulas in Python

Many of my articles include code which implements mathematical formulas, and as well as the Python code itself I usually include the formulas in traditional mathematical notation. These are typical examples, the quadratic equation and the quadratic formula to solve it.
If you find or are given a mathematical expression in this format to implement in code the necessary steps or techniques might not be obvious. In this article I will discuss many of the more common bits of mathematical notation and illustrate how to translate them to Python using real-world examples like the two shown above. Unlike with most of my articles there are no separate code files, just small code snippets which you can copy and paste to try out or use as you wish. I won't explain the mathematics in detail as that isn't the purpose of this article, but will just concentrate on the mathematical notation and its Python equivalents.
Variable Names
Formulas and equations are almost certain to be delivered to you with single-letter variable names, x, y, Θ etc. Using single letters for programming certainly isn't considered good practice but my opinion is that is justified when implementing mathematical expressions which exist outside of the code, even if only in the specifications or documentation of the software you are writing.
If you are writing code with a significant mathematical content then it is likely to be of a general purpose nature with no specific names that can be attached to variables. As an example this is the formula for the arithmetic mean which I'll look at later.
The formula is identical whether you are calculating the mean of people's heights, exam scores or server response times so it wouldn't make sense to call a variable number_of_exam_scores instead of n. In this case I would probably use n, x and i as in the formula but you might prefer to use, for example, count, current and index. However, x̄ is a terrible name for a variable* so I'd probably go with mean. At the end of the day just do what seems reasonable in a specific situation considering who is likely to read the code, comment anything that might be misunderstood, and for larger projects set out and document some standards.
* x̄ is one of those characters that requires two Unicode codes, U+0078 U+0304.
Implicit Multiplication
Now let's get into writing actual code and I'll starts with something simple. You may well be aware that in a formula like this:
the values of m and a are multiplied, with multiplication being the default operation if none is specified. This is known as implicit multiplication but obviously we can't do this in Python. If we have variables called m and a and smush them together then Python will complain that there is no variable called ma. The solution is simple and obvious:
F = m * a Well I told you it was simple! (If you are interested the formula above is Newton's Second Law of Motion and specifies the relationship between force F, mass m and acceleration a.)
Operator Precedence
If you begin to learn any programming language using a formal and methodical approach then the topic of the mathematical operators +, -, * and / will come up pretty quickly, closely followed by their precedence or order in which they are evaluated.
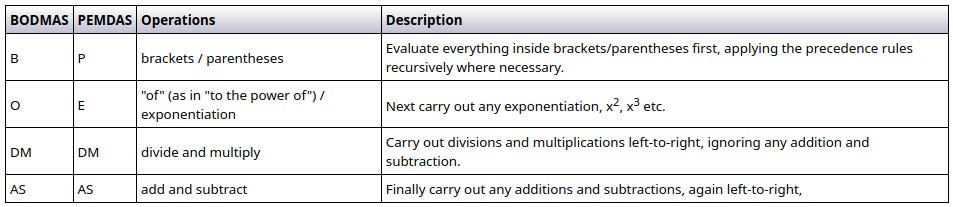
There are a couple of equivalent mnemonics to remember operator precedence, BODMAS and PEMDAS which you may well already know about. They are described in the table below.
The good news is that Python is fully aware of operator precedence and applies them without you having to do anything specific. Here are a couple of very simple examples.
y = 23 + 7 / 2
z = (23 + 7) / 2 In the first line division is carried out first so this evaluates to 26.5. In the second line brackets force addition to be evaluated first so the result is 15. I haven't included powers or exponents in this section as it's a topic that deserves a section to itself.
Exponents
Let's look at the quadratic equation shown at the beginning of the article.
In this form it is an equation, just a statement of fact rather than a description of how to calculate an unknown value. Let's write it in a form which can be used to calculate the values of an unknown variable y using known values of x. This is the sort of thing you are likely to need to implement in code.
This formula raises x to the power of 2 for which Python uses the ** operator, and we already know from the previous section that if we implement an expression in Python the interpreter will handle operator precedence automatically. This is the above formula in Python.
y = a*x**2 + b*x + c Having no spaces either side of the * but spaces either side of the + is just how I like to do things, and it does make the code more closely resemble the original notation. A calculation consisting of one or more multiplications and/or divisions is known as a term, and they can be joined by additions or subtractions as here. The spacings or lack of emphasise the BODMAS/PEMDAS rule.
Square Roots, the Plus and Minus Symbol, and Division
This is the quadratic formula shown earlier.
There are a few new things to think about here.
The plus and minus sign ± indicates that there are actually two separate formulas represented here, the first adds the second term above the line and the second subtracts it.
You probably recognise the square root symbol √, but we need to be careful to take the square root of everything under the symbol's horizontal line.
Finally, everything above the long horizontal line is divided by 2a. That's perfectly clear from the formula above but we need to be careful to get this right in Python.
Let's write the top half of the formula first, with the plus option.
(-b) + (b**2 - 4*a*c)**0.5 I have parenthesised -b for clarity, and the entire expression that is square-rooted is also parenthesised. For the square root calculation I have used **0.5 ("to the power of one half") as I think it's more concise. However, you may prefer to use the math.sqrt method:
(-b) + math.sqrt(b**2 - 4*a*c) Now all we need to do is wrap all of the above in parentheses and divide by 2a, which is also parenthesised otherwise the division would be evaluated before the multiplication.
((-b) + math.sqrt(b**2 - 4*a*c)) / (2*a) This is the minus version
((-b) - math.sqrt(b**2 - 4*a*c)) / (2*a) The code above fully implements the quadratic formula, both plus and minus. However, to be useful we need to use them to calculate values of x. As a bit of bonus code I have written a Python function which takes a, b and c as arguments and calculates the two possible values of x in a dictionary.
def quadratic_formula(a: float, b: float, c: float) -> float:
x_plus = ((-b) + math.sqrt(b**2 - 4*a*c)) / (2*a)
x_minus = ((-b) - math.sqrt(b**2 - 4*a*c)) / (2*a)
return {"x_plus": x_plus, "x_minus": x_minus} Constants: π and e
I have already mentioned constants in the context of the a, b and c values used in the quadratic equation. However, these are only constant in a particular situation. In this section I'll look at two constants that really are just that, constant, everywhere and for all of time.
They both live in Python's math module so you just need to import math and type math.[constant name]. As an alternative you can use the from/import syntax which lets you use the constant without the math namespace. This is a matter of personal choice and the latter makes code more concise.
These are the constants currently provided by the math module. They are both irrational numbers so go on forever if you let them, and I have also shown the values to the precision provided by Python, 15dp in each case.
(math also includes tau (the Greek letter τ) or 2π which is sometimes more convenient to use that π but rather obscure.)
This snippet imports and prints both constants.
import math
print(math.pi)
print(math.e)This is the alternative syntax. Always remember that there is a danger of inadvertently reusing variable names that have been severed from their module names.
from math import pi, e
print(pi)
print(e) Here is a code snippet which calculates the area of a circle with radius r.
r = 12
a = math.pi*r**2 # 452.3893421 Constants Not in math
As well as pi and e discussed in the previous section there is a plethora of other constants used across mathematics, science, technology and other fields. In this section I'll use just two as examples: c, the speed of light, and G, the universal gravitational constant.
If you need to use a constant, c, G or anything else, it's tempting to just hard code it as and when it is actually being used although of course this is a Bad Idea™. A Better Idea™ would be to hard code constants somewhere at the top of the file. If you are going to need stuff like this a lot then you could also consider creating a separate module just for constants which you could use something like this:
import physics_constants as const
const.c
const.GYou could be a lot more verbose with stuff like:
const.speed_light_ms but anyone writing and reading code using constants such as this will probably be familiar with the meaning of c etc. so wouldn't need the long names which would make the code much more cumbersome.
The Python convention is to use all upper case for constants but with the speed of light for example the use of the lower-case c is a universal convention which I feel should be respected. Also, the upper-case C is the standard symbol for electrical capacitance so there is room for a clash of variable names (if you are unfortunate enough to be using the speed of light and electrical capacitance in the same code). I have therefore used c in this code.
The formula below is Newton's Law of Universal Gravitation which is used to calculate the force of gravity between two objects with masses m1 and m2 and with a distance or r between their centres of mass. These are variables but the G which we are interested in here is a constant with the value 6.67408 * 10**-11 or 0.0000000000667408*. (The unit is m3 ⋅ kg-1 ⋅ s-2)
Let's assume G is hard-coded in the file it is used in like this:
G = 6.67408 * 10**-11 It can then be used in an implementation of the Law of Universal Gravitation like this (assuming m1, m2 and r already exist).
F = G * ( (m1 * m2) / (r**2 ) ) You may recognise the following as Einstein's famous equation describing the relationship between a certain mass m of matter and its corresponding (huge) amount of energy.
The mass m is a variable so we just need to hard-code the value of c somewhere, for example:
c = 299_792_458 # metres per second Python lets us use underscores to make longer numbers easier to read. Once we have c in place it is simple to code the formula, assuming m already exists:
E = m*c**2 Trigonometric Functions
In this section I'll cover six trigonometric functions. The first three, sin, cos and tan, calculate the ratios of the sides of a right triangle from a known angle, and their three inverses, asin, acos and atan, calculate an angle from a known ratio.
It is critical here to know that these functions use radians as their unit of angle, not degrees. The first three take angles in radians as arguments, and the second three return angles in radians.
Python provides a pair of functions for converting between degrees and radians, and I have written an article on the topic of handling the whole process of using degree and radian units which you may find useful. For the rest of this section I'll assume that all angles are in radians.
The first three formulas below calculate unknown sides of a triangle using one known angle θ and one known side. The sides are o(pposite), a(djacent) and h(ypotenuse).
Coding these in Python is straightforward but remember to import math. I have used angle as a variable name instead of θ but see the Greek Letters section below.
o = h * math.sin(angle)
a = h * math.cos(angle)
o = a * math.tan(angle) The three inverse functions asin, acos and atan (or arcsin, arccos and arctan to give them their full names) calculate angles from the ratios of known sides.
The Python for these is equally straightforward:
angle = math.asin(o/h)
angle = math.acos(a/h)
angle = math.atan(o/a)Factorial!
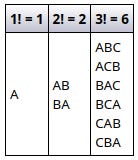
You might have come across factorials and their symbol ! as the classic example of recursion, or calling a function from itself. They crop up in some unexpected places but the simplest use is to calculate how many different ways n objects can be arranged, the answer being n!. This table shows the ways of arranging 1, 2 and 3 objects, in this case letters.
Fortunately we don't have to do the recursion thing, or even a for loop, as Python provides a function for us. This snippet shows it calculating a few factorials.
import math
for n in range(1,9):
print(f"{n}! = {math.factorial(n)}") This is the output. As you can see the results get very big very quickly! (See what I did there...?)
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320 Summation Σ
This is the formula to calculate the arithmetic mean of a dataset, commonly known as the "average" although this is imprecise as there are several types of average. The version on the right is more intuitive and slightly closer to how the calculation is actually carried out, either manually or in code. However, the version on the left using Σ is more compact and precise.
In practice you wouldn't need to implement this formula in Python as the built-in statistics library and NumPy both have methods to do it for you. However, this is just a simple example which can be generalised to any expression using Σ summation.
Aside from calculating the arithmetic mean, Python and NumPy both have sum functions for totalling an iterable and these should be used when you see Σ in a formula. There is an exception to this: occasionally the symbol over the summation sign might be infinity ∞, usually seen in infinite series which converge on an increasingly more accurate result. For this article though I'll assume you want to sum actual data, and the first code snippet does this in plain Python.
data = [23.8,55.0,83.9,28.7,19.5,90.8,45.6]
print(sum(data)) The second snippet does the same thing using NumPy.
import numpy as np
data = np.array([23.8,55.0,83.9,28.7,19.5,90.8,45.6])
print(np.sum(data)) Greek Letters
Greek letters crop up quite often in mathematics, and it is common for a certain Greek letter to be the de facto standard notation for a quantity in a specific field. An example is λ or lambda which is widely used for wavelength. This is the formula for calculating wavelength from velocity and frequency.
This raises a bit of conundrum. If you want to keep your code as close to the mathematics it might seem reasonable to use Greek letters as variable names:
λ = v/f However, any characters you cannot type directly with your keyboard are a pain. I know this because I use them far too often myself! I cannot give a definitive answer to the conundrum but I'll just say use Greek letters if you really feel it's necessary for your code to follow the source notation as closely as possible, and the sort of people who read your code are likely to be of a similar mindset. But if in doubt do this:
wavelength = velocity/frequency If you do decide to use Greek letters then you might like to keep a reference handy so that you can copy and paste them. I have the Wikipedia article on the Greek alphabet bookmarked for that purpose.
Conclusion
This article has covered a number of the most common types of mathematical notation you are likely to come across. If you come across any more esoteric or specialised formulas please let me know and I will have a go at implementing them in Python.
No AI was used in the creation of the code, text or images in this article.