Plotting Parametric Equations with Python
In this article on Polar Plots I contrasted the plotting of functions which map values on the x-axis of a graph to values on the y-axis with calculating and plotting values from angles around the origin. In this article I'll introduce a third way of calculating coordinates, one which uses separate functions for each axis and a separate variable called a parameter which gives these equations their name.
I'll plagiarise the bit of my own polar plots article on cartesian coordinates and then describe parametric equations in more detail.
"You are probably familiar with plotting functions on a Cartesian Plane, where for every point on the horizontal x-axis you can calculate a corresponding coordinate on the y-axis using a function of the form:"
y = f(x)
"For example if you plot"
y = x2
"you will get something like this."
"The above was drawn by iterating x from -10 to 10, and for each value of x calculating the corresponding value of y. Each point x,y is then plotted on the graph."
OK, back to original content!
As I mentioned we use a variable called a parameter (often denoted by t, evidently because it often represents time) which is iterated over a range, and for each iteration two functions are evaluated, one for the x coordinate and one for the y coordinate. The functions perform some sort of calculation using the values of t and can be as complex as necessary, including multiplication to change the appearance or size of the resulting graph, or addition/subtraction to move the points around. Just to give a flavour of what the equations look like here are a very simple pair to draw a circle. In this case t is an angle and we'd iterate from 0° to 360° so there are close similarities with drawing a circle using a polar plot.
x = cos(t)
y = sin(t)
Each equation starts with x = or y = but to the right of the equals sign you can do anything you like as long as you carry out some sort of calculation using t.
The Project
This project consists of the following files:
parametricplotter.py
parametricequations.py
parametricdemo.py
which you can clone/download from the GitHub repository.
The Code
This project uses Numpy which is a very popular Python library providing an easy to use but fast and efficient array data structure. My usage here is very simple and I'll describe it as we go, but if you're not already a Numpythonista you might like to visit the Numpy site and PyPI page.
https://pypi.org/project/numpy/
The plot is created with Matplotlib, another very popular Python library which works very well with Numpy and is also a quick "pip" away. These are Matplotlib's site and PyPI entry.
https://pypi.org/project/matplotlib
The parametricplotter.py file contains a single function called plot which is at the heart of the project.
parametricplotter.py
import numpy as np
import matplotlib.pyplot as plt
def plot(xEquation, yEquation, tStart, tStop, tStep, colour, title):
'''
Plots parametric equation pairs
calculating x and y coordinates
using parameter argument t.
The equations are evaluated over the
specified range with the specified interval.
'''
# array of t values
tValues = np.arange(tStart, tStop, tStep)
# create versions of functions which can be applied to arrays
xEquation = np.vectorize(xEquation)
yEquation = np.vectorize(yEquation)
# evaluate functions to get x and y coordinates
x = xEquation(tValues)
y = yEquation(tValues)
# load of routine Matplotlib stuff
ax = plt.figure().add_subplot()
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.grid()
ax.set_aspect('equal')
# by default axis limits are set to accomodate values
# uncomment these lines to set specific values
# and edit as necessary
# ax.set_xlim(-5.0,5.0)
# ax.set_ylim(-5.0,5.0)
ax.plot(x, y, color=colour)
plt.title(title)
plt.show()At the top of the file numpy and matplotlib are imported, the np and plt aliases being pretty much a de-facto standard which most people use.
The first two arguments are the functions to calculate x and y coordinates from parameter values. The next two are the start and end values of the parameter and are angles in radians. These are often the radian equivalents of 0° to 360° but not always, as in the case of the spiral example. The next value is the step or interval of the parameter values and needs to be chosen to give a smooth curve but without an unnecessarily large number of individual points. The final two arguments specify the colour of the curve and the title to display at the top.
The first half of the plot function creates a pair of Numpy arrays containing x and y coordinates to plot. Firstly we create a set of parameter values called tValues which is very simple with Numpy's arange method: just specify the start, stop and step.
A very powerful feature of Numpy is the ability to apply a function to an entire array in a single statement without a loop. However, such functions have to be specially created which can be done using the vectorize method. This takes a normal function and wraps it to make it Numpy friendly.
Lastly we just call the two vectorized functions with the parameter or T values to created the necessary x and y coordinates as Numpy arrays.
The second half of the function does the actual plotting, the first line creating a new plot and the next four lines setting a few aesthetic properties.
The next line is delightfully simple: just throw the coordinate arrays and colour at the plot method. Bear in mind though that there are other arguments you can add if necessary. After that we just set the title and show the plot.
The parametricequations.py file contains a few sample equations.
parametricequations.py
import math
# edit multiplier to change radius
# edit 0 to move circle horizontally and vertically
circle = {"xFunction": lambda t: (math.cos(t) * 1.0) + 0.0,
"yFunction": lambda t: (math.sin(t) * 1.0) + 0.0,
"tStart": 0,
"tEnd": (2 * math.pi) + (math.pi / 32),
"tStep": math.pi / 32,
"colour": "#FF0000",
"name": "Circle"}
# edit multiplier in xFunction to change width
# edit multiplier in yFunction to change height
ellipse = {"xFunction": lambda t: 1.0 * math.cos(t),
"yFunction": lambda t: 0.5 * math.sin(t),
"tStart": 0,
"tEnd": (2 * math.pi) + (math.pi / 32),
"tStep": math.pi / 32,
"colour": "#00C000",
"name": "Ellipse"}
cardioid = {"xFunction": lambda t: math.cos(t) * (1 + math.cos(t)),
"yFunction": lambda t: math.sin(t) * (1 + math.cos(t)),
"tStart": 0,
"tEnd": (2 * math.pi) + (math.pi / 32),
"tStep": math.pi / 32,
"colour": "#800080",
"name": "Cardioid"}
# edit multiplier in xFunction to change width
# edit multiplier in yFunction to change height
spiral = {"xFunction": lambda t: math.cos(t) * (1.0 * t),
"yFunction": lambda t: math.sin(t) * (1.0 * t),
"tStart": 0,
"tEnd": (10 * math.pi) + (math.pi / 32),
"tStep": math.pi / 32,
"colour": "#800080",
"name": "Spiral"}
# the multiplier is half the number of petals
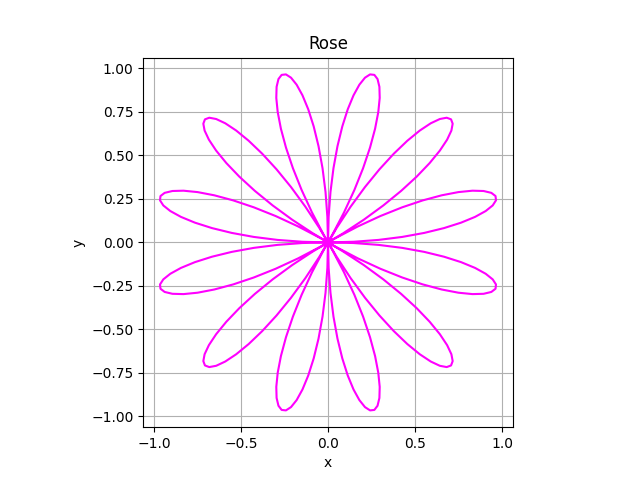
rose = {"xFunction": lambda t: math.cos(t) * (math.sin(t * 6)),
"yFunction": lambda t: math.sin(t) * (math.sin(t * 6)),
"tStart": 0,
"tEnd": (2 * math.pi) + (math.pi / 128),
"tStep": math.pi / 128,
"colour": "#FF00FF",
"name": "Rose"}
Lissajous_1_2 = {"xFunction": lambda t: math.sin(1 * t + (math.pi / 2)),
"yFunction": lambda t: math.sin(2 * t),
"tStart": 0,
"tEnd": (2 * math.pi) + (math.pi / 128),
"tStep": math.pi / 128,
"colour": "#FF8000",
"name": "Lissajous Curve 1:2"}
Lissajous_3_2 = {"xFunction": lambda t: math.sin(3 * t + (math.pi / 2)) ,
"yFunction": lambda t: math.sin(2 * t),
"tStart": 0,
"tEnd": (2 * math.pi) + (math.pi / 128),
"tStep": math.pi / 128,
"colour": "#FF8000",
"name": "Lissajous 3:2"}
Lissajous_3_4 = {"xFunction": lambda t: math.sin(3 * t + (math.pi / 2)),
"yFunction": lambda t: math.sin(4 * t),
"tStart": 0,
"tEnd": (2 * math.pi) + (math.pi / 128),
"tStep": math.pi / 128,
"colour": "#FF8000",
"name": "Lissajous 3:4"}
Lissajous_5_4 = {"xFunction": lambda t: math.sin(5 * t + (math.pi / 4)),
"yFunction": lambda t: math.sin(4 * t),
"tStart": 0,
"tEnd": (2 * math.pi) + (math.pi / 128),
"tStep": math.pi / 128,
"colour": "#FF8000",
"name": "Lissajous 5:4"}Each of the entries in this file is a dictionary of arguments to pass to the parametricplotter's plot function. It's not essential to use these as I'll show in a moment but it's a convenient way of storing the stuff we need. If you invent or discover any more please let me know and fork the repository.
The functions are lambdas and the parameters all start at 0 which is the 3 o'clock position. The end values are either 360° in radians or multiples of 360°. Note they have a bit added on to complete the loop.
The names of the Lissajous dictionaries include the hard-coded multipliers. I'm planning a separate article on the subject of Lissajous curves so won't go into detail here.
The final file is parametricdemo.py which puts the code above to work.
import math
import parametricplotter as pp
import parametricequations as pe
def main():
'''
Pick up one of the functions from the
dictionary in parametricequations.py
Use its values as arguments for the
parametricplotter's plot function
It is not necessary to use the
parametricequations dictionary.
Any arguments can be used as in the
commented example.
'''
# Use functions in parametricequations.py
func = pe.circle
# func = pe.ellipse
# func = pe.cardioid
# func = pe.spiral
# func = pe.rose
# func = pe.Lissajous_1_2
# func = pe.Lissajous_3_2
# func = pe.Lissajous_3_4
# func = pe.Lissajous_5_4
pp.plot(func["xFunction"],
func["yFunction"],
func["tStart"],
func["tEnd"],
func["tStep"],
func["colour"],
func["name"])
# Use lambdas coded into function call
# pp.plot(xEquation=lambda t: (math.cos(t) * 1.0) + 0.0,
# yEquation=lambda t: (math.sin(t) * 1.0) + 0.0,
# tStart=0,
# tStop=(2 * math.pi) + (math.pi / 32),
# tStep=math.pi / 32,
# colour="#00C000",
# title="A Nice Green Circle")
if __name__ == "__main__":
main()This file imports parametricplotter and parametricequations with concise aliases. In main the func variable is assigned to one of the dictionaries in parametricequations, and the various bits and pieces of the dictionary are used as arguments to pp.plot.
I mentioned that you don't have to use the stuff in parametricequations but can code the values directly into a function call. The commented-out section at the end on main does just that.
Running the Program
The coding is now complete so let's run it:
python3 parametricdemo.py
You can choose which functions to use by uncommenting the appropriate line in main starting func =, or uncomment the final section where lambdas are hard-coded into the call to pp.plot.
These are the plots from the various types of parametric equation.
Conclusion
The equations shown in this article are just a few simple examples. If you create any more please let me know in the comments or add them to a Github fork.
As I mentioned Lissajous curves deserve their own follow-up article so watch this space.